题目内容
20. 如图,已知四边形ABCD内接于圆,延长AB和DC交于E,EG平分∠E,且与BC、AD别相交于F、G.求证:∠CFG=∠DGF.
如图,已知四边形ABCD内接于圆,延长AB和DC交于E,EG平分∠E,且与BC、AD别相交于F、G.求证:∠CFG=∠DGF.
分析 由A、B、C、D四点共圆,知∠ADC=∠EBF,由∠BEF=∠DEG,能证明∠CFG=∠DGF.
解答 证明:∵A、B、C、D四点共圆,
∴∠ADC=∠EBF,
∵EG平分∠AED,∴∠BEF=∠DEG,
∴∠EGD=∠EFB,
∵∠CFG=∠EFB,∠EGD=∠DGF,
∴∠CFG=∠DGF
点评 本题考查与圆有关的比例线段的求法,解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
20.一直线l绕其上一点P逆时针旋转15°后得到直线$\sqrt{3}x$-y-$\sqrt{3}$=0,再逆时针旋转75°后得到直线x+y-1=0,则l的方程为( )
| A. | x-y-1=0 | B. | x+y-1=0 | C. | $\sqrt{3}$x+y-$\sqrt{3}$=0 | D. | $\sqrt{3}$x-y+$\sqrt{3}$=0 |
9.一椭圆的中心在原点,焦点F1、F2在x轴上,点P是椭圆上一点,线段PF1与y轴的交点M是该线段的中点,若|PF2|=|MF2|,则椭圆的离心率等于( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{\sqrt{3}}{3}$ |
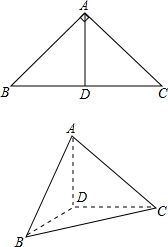 如图,在△ABC中,∠ABC=45°,∠BAC=90°,AD是BC上的高,沿AD把△ABD折起,使∠BDC=90°,若BD=1,求三棱锥D-ABC的表面积.
如图,在△ABC中,∠ABC=45°,∠BAC=90°,AD是BC上的高,沿AD把△ABD折起,使∠BDC=90°,若BD=1,求三棱锥D-ABC的表面积.