题目内容
【题目】椭圆的中心在原点O,短轴长为 ![]() ,左焦点为F(﹣c,0)(c>0),直线
,左焦点为F(﹣c,0)(c>0),直线 ![]() 与x轴交于点A,且
与x轴交于点A,且 ![]() ,过点A的直线与椭圆相交于P,Q两点.
,过点A的直线与椭圆相交于P,Q两点. 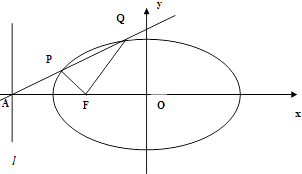
(1)求椭圆的方程.
(2)若 ![]() ,求直线PQ的方程.
,求直线PQ的方程.
【答案】
(1)解:设 ![]() ,
,
则 ![]() ,
, ![]() ,
,
解得a2=4,c=1,
所以椭圆方程为 ![]() .
.
(2)解:设PQ的方程为y=k(x+4),P(x1,y1),Q(x2,y2),F(﹣1,0)
∵PF⊥QF,∴(x1+1)(x2+1)+y1y2=0,
即 ![]() ,
, ![]() .
.
联立得 ![]()
消去y,得(3+4k2)x2+32k2x+64k2﹣12=0,
由△>0,得 ![]() .
.
∴ ![]() .
.
代入(*)式化简,得8k2=1,∴ ![]() .
.
则直线PQ的方程为 ![]() .
.
【解析】(1)设 ![]() ,由题意可得
,由题意可得 ![]() ,
, ![]() ,c2=a2+b2 , 解出即可;(2)设PQ的方程为y=k(x+4),P(x1 , y1),Q(x2 , y2),F(﹣1,0),把方程与椭圆方程联立得到根与系数的关系,再利用
,c2=a2+b2 , 解出即可;(2)设PQ的方程为y=k(x+4),P(x1 , y1),Q(x2 , y2),F(﹣1,0),把方程与椭圆方程联立得到根与系数的关系,再利用 ![]()
![]() 即可得出.
即可得出.
【考点精析】关于本题考查的椭圆的标准方程,需要了解椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() 才能得出正确答案.
才能得出正确答案.

练习册系列答案
相关题目