题目内容
【题目】在直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() ,若圆
,若圆![]()
![]() 的一条切线与椭圆
的一条切线与椭圆![]() 有两个交点
有两个交点![]() ,且
,且![]() .
.

(1)求圆![]() 的方程;
的方程;
(2)已知椭圆![]() 的上顶点为
的上顶点为![]() ,点
,点![]() 在圆
在圆![]() 上,直线
上,直线![]() 与椭圆
与椭圆![]() 相交于另一点
相交于另一点![]() ,且
,且![]() ,求直线
,求直线![]() 的方程.
的方程.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)先讨论切线斜率存在时,设圆的切线为![]() ,点
,点![]() ,由直线与椭圆方程联立方程组后消元韦达定理可得
,由直线与椭圆方程联立方程组后消元韦达定理可得![]() ,代入
,代入![]() 可得出
可得出![]() 的关系,从而可求得圆心到此直线的距离即圆半径,得圆方程,验证当斜率不存在的直线
的关系,从而可求得圆心到此直线的距离即圆半径,得圆方程,验证当斜率不存在的直线![]() 也满足题意;
也满足题意;
(2)设点![]() ,由
,由![]() ,得
,得 ,由
,由![]() 分别在椭圆和圆上,联立方程组解得
分别在椭圆和圆上,联立方程组解得![]() 后可得直线方程.
后可得直线方程.
(1)设圆的切线为![]() ,点
,点![]() .由方程组
.由方程组 得
得![]() ,得
,得![]() .因为
.因为![]() ,所以
,所以![]() ,即
,即![]() .又因为点
.又因为点![]() 在直线
在直线![]() 上,所以
上,所以![]() ,即
,即![]() .所以
.所以![]() ,化简得
,化简得![]() ,所以圆
,所以圆![]() 的半径
的半径![]() ,所以圆
,所以圆![]() 的方程为
的方程为![]() .此时,当切线为
.此时,当切线为![]() 时,易证满足
时,易证满足![]() .
.
(2)设点![]() ,点
,点![]() ,由
,由![]() ,得
,得 .代入椭圆和圆得
.代入椭圆和圆得 解得
解得 或者
或者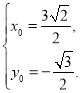 所以点
所以点 或
或
.故直线![]() 的方程为
的方程为![]() 或
或![]() ..
..

【题目】依法纳税是每个公民应尽的义务,个人取得的所得应依照《中华人民共和国个人所得税法》向国家缴纳个人所得税(简称个税).2019年1月1日起,个税税额根据应纳税所得额、税率和速算扣除数确定,计算公式为:
个税税额=应纳税所得额×税率-速算扣除数.
应纳税所得额的计算公式为:
应纳税所得额=综合所得收入额-免征额-专项扣除-专项附加扣除-依法确定的其他扣除.
其中免征额为每年60000元,税率与速算扣除数见下表:
级数 | 全年应纳税所得额所在区间 | 税率( | 速算扣除数 |
1 |
| 3 | 0 |
2 |
| 10 | 2520 |
3 |
| 20 | 16920 |
4 |
| 25 | 31920 |
5 |
| 30 | 52920 |
6 |
| 35 | 85920 |
7 |
| 45 | 181920 |
备注:
“专项扣除”包括基本养老保险、基本医疗保险、失业保险等社会保险费和住房公积金。
“专项附加扣除”包括子女教育、继续教育、大病医疗、住房贷款利息或者住房租金、赡养老人等支出。
“其他扣除”是指除上述免征额、专项扣除、专项附加扣除之外,由国务院决定以扣除方式减少纳税的优惠政策规定的费用。
某人全年综合所得收入额为160000元,假定缴纳的基本养老保险、基本医疗保险、失业保险等社会保险费和住房公积金占综合所得收入额的比例分别是![]() ,
,![]() ,
,![]() ,
,![]() ,专项附加扣除是24000元,依法确定其他扣除是0元,那么他全年应缴纳综合所得个税____元.
,专项附加扣除是24000元,依法确定其他扣除是0元,那么他全年应缴纳综合所得个税____元.
【题目】一只红玲虫的产卵数![]() 和温度
和温度![]() 有关.现收集了7组观测数据如下表:
有关.现收集了7组观测数据如下表:
温度 | 21 | 23 | 25 | 27 | 29 | 32 | 35 |
产卵数 | 7 | 11 | 21 | 24 | 66 | 115 | 325 |
为了预报一只红玲虫在![]() 时的产卵数,根据表中的数据建立了
时的产卵数,根据表中的数据建立了![]() 与
与![]() 的两个回归模型.模型①:先建立
的两个回归模型.模型①:先建立![]() 与
与![]() 的指数回归方程
的指数回归方程![]() ,然后通过对数变换
,然后通过对数变换![]() ,把指数关系变为
,把指数关系变为![]() 与
与![]() ;模型②:先建立
;模型②:先建立![]() 与
与![]() 的二次回归方程
的二次回归方程![]() ,然后通过变换
,然后通过变换![]() ,把二次关系变为
,把二次关系变为![]() 与
与![]() 的线性回归方程:
的线性回归方程:![]() .
.
(1)分别利用这两个模型,求一只红玲虫在![]() 时产卵数的预测值;
时产卵数的预测值;
(2)你认为用哪个模型得到的预测值更可靠?并说明理由.(参考数据:模型①的残差平方和![]() ,模型①的相关指数
,模型①的相关指数![]() ;模型②的残差平方和
;模型②的残差平方和![]() ,模型②的相关指数
,模型②的相关指数![]() ;
;![]() ,
,![]() ,
,![]() ;
;![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)