题目内容
设函数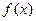 是定义在R上的奇函数,对任意实数
是定义在R上的奇函数,对任意实数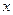 有
有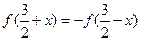 成立.
成立.
(1)证明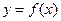 是周期函数,并指出其周期;
是周期函数,并指出其周期;
(2)若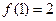 ,求
,求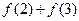 的值;
的值;
(3)若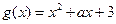 ,且
,且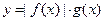 是偶函数,求实数
是偶函数,求实数 的值.
的值.
解(1)由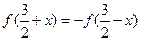 ,且
,且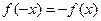 知
知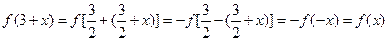 ,
,
所 以
以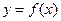 是周期函数,且
是周期函数,且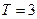 是其一个周期.
是其一个周期.
(2)因为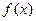 为定义在R上的奇函数,所以
为定义在R上的奇函数,所以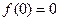 ,且
,且 ,又
,又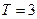 是
是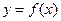 的一个周期,所以
的一个周期,所以 ;
;
(3)因为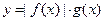 是偶函数,且可证明
是偶函数,且可证明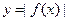 是偶函数,所以
是偶函数,所以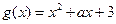 为偶函数,即
为偶函数,即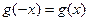 恒成立.
恒成立.
于是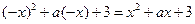 恒成立,于是
恒成立,于是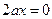 恒成立
恒成立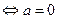 ,
,
所以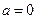 为所求.
为所求.
解析

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
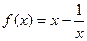

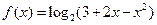 . (
. ( 1) 求函数
1) 求函数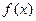 的定义域;(2) 求证
的定义域;(2) 求证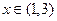 上是减函数;(3) 求函数
上是减函数;(3) 求函数 域.
域.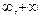 )上的单调性,并用定义证明。
)上的单调性,并用定义证明。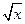 -2(x≥0)及f2(x)=4-6·
-2(x≥0)及f2(x)=4-6·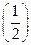 x(x≥0)是否属于集合A?并简要说明理由;
x(x≥0)是否属于集合A?并简要说明理由;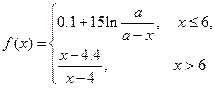
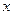 表示某学科知识的学习次数(
表示某学科知识的学习次数(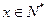 ),
),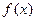 表示对该学科知识的掌握程度,正实数a与学科知识有关
表示对该学科知识的掌握程度,正实数a与学科知识有关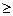 7时,掌握程度的增长量f(x+1)- f(x)总是下降;
7时,掌握程度的增长量f(x+1)- f(x)总是下降; 1,127]
1,127] 85%,请
85%,请 确定相应的学科.
确定相应的学科. 满足不等式
满足不等式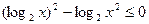 ,求函数
,求函数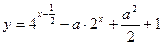 的最小值.
的最小值.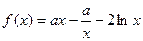
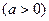 ,若函数
,若函数 在其定义域内为单调函数,求
在其定义域内为单调函数,求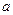 的取值范围.
的取值范围.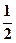 ,1]时,不等式f (ax+1)≤f (x-2)恒成立,则求实数a的取值范围?
,1]时,不等式f (ax+1)≤f (x-2)恒成立,则求实数a的取值范围?