题目内容
6.已知实数x、y满足$\left\{\begin{array}{l}{x+y≥2}\\{x-y≤2}\\{0≤y≤3}\end{array}\right.$,则z=2x-y的取值范围是( )| A. | [-5,7] | B. | [5,7] | C. | [4,7] | D. | [-5,4] |
分析 由约束条件作出可行域,化目标函数为直线方程的斜截式,数形结合得到最优解,联立方程组求得最优解的坐标,代入目标函数得答案.
解答 解:由约束条件$\left\{\begin{array}{l}{x+y≥2}\\{x-y≤2}\\{0≤y≤3}\end{array}\right.$作出可行域如图,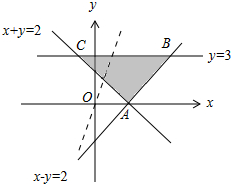
联立$\left\{\begin{array}{l}{y=3}\\{x+y=2}\end{array}\right.$,解得C(-1,3),
联立$\left\{\begin{array}{l}{y=3}\\{x-y=2}\end{array}\right.$,解得B(5,3),
化目标函数z=2x-y为y=2x-z,
由图可知,当直线y=2x-z过B时,直线在y轴上的截距最小,z有最大值为2×5-3=7;
当直线y=2x-z过C时,直线在y轴上的截距最大,z有最小值为2×(-1)-3=-5.
∴z=2x-y的取值范围是[-5,7].
故选:A.
点评 本题考查简单的线性规划,考查了数形结合的解题思想方法,是中档题.

练习册系列答案
相关题目
14.若曲线C1:x2+y2-2x=0与曲线C2:x(y-mx-m)=0有三个不同的公共点,则实数m的取值范围是( )
| A. | (0,$\sqrt{3}$) | B. | (-$\sqrt{3}$,0)∪(0,$\sqrt{3}$) | C. | (0,$\frac{{\sqrt{3}}}{3}$) | D. | (-$\frac{{\sqrt{3}}}{3}$,0)∪(0,$\frac{{\sqrt{3}}}{3}$) |
11.已知点P(x0,y0)在直线L:4x+5y+20=0的左下方,则4x0+5y0+20的值( )
| A. | 一定等于0 | B. | 一定小于0 | C. | 一定大于0 | D. | 符号不能确定 |
18.已知函数y=lg(x2-3x+2)的定义域为A,y=lg(x-1)+lg(x-2)的定义域为B,则( )
| A. | A∩B=∅ | B. | A=B | C. | A?B | D. | B?A |
15.方程xy2-x2y=8x所表示的曲线( )
| A. | 关于y轴对称 | B. | 关于y+x=0对称 | C. | 关于原点对称 | D. | 关于x-y=0对称 |
16.某个几何体的三视图如图所示,则该几何体的体积是( )


| A. | 30 | B. | 40 | C. | 24 | D. | 72 |