题目内容
设函数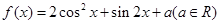 .
.
(1)求函数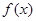 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;
(2)当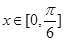 时,
时,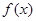 的最大值为2,求
的最大值为2,求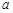 的值,并求出
的值,并求出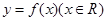 的对称轴方程.
的对称轴方程.
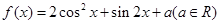 .
.(1)求函数
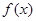 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;(2)当
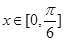 时,
时,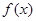 的最大值为2,求
的最大值为2,求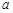 的值,并求出
的值,并求出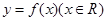 的对称轴方程.
的对称轴方程.(1)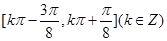 ;(2)
;(2)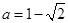 ,
,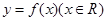 的对称轴方程为
的对称轴方程为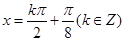 .
.
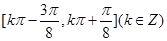 ;(2)
;(2)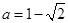 ,
,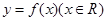 的对称轴方程为
的对称轴方程为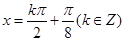 .
.试题分析:(1)求函数
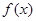 的单调递减区间,首先对
的单调递减区间,首先对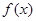 进行恒等变化,将它变为一个角的一个三角函数,然后利用三角函数的单调性,来求函数
进行恒等变化,将它变为一个角的一个三角函数,然后利用三角函数的单调性,来求函数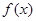 的单调递减区间,本题首先通过降幂公式降幂,及倍角公式,得到
的单调递减区间,本题首先通过降幂公式降幂,及倍角公式,得到 与
与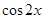 的关系式,再利用两角和的三角函数公式,得到
的关系式,再利用两角和的三角函数公式,得到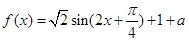 ,从而得到单调递增区间;(2)求
,从而得到单调递增区间;(2)求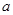 的值,由已知当
的值,由已知当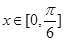 时,
时,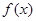 的最大值为2,由
的最大值为2,由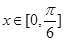 ,得
,得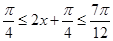 ,当
,当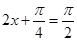 ,即
,即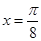 ,
,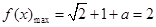 ,可求
,可求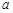 的值,求
的值,求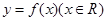 的对称轴方程,即
的对称轴方程,即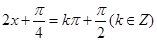 ,解出
,解出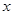 ,即得对称轴方程.
,即得对称轴方程.试题解析:(1)
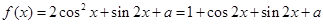
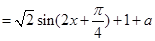 2分
2分则
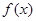 的最小正周期
的最小正周期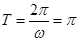 , 4分
, 4分且当
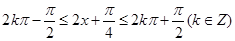 时
时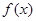 单调递增.
单调递增.即
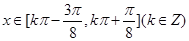 为
为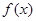 的单调递增区间
的单调递增区间(写成开区间不扣分). 6分
(2)当
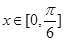 时
时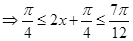 ,当
,当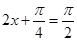 ,即
,即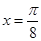 时
时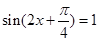 .
.所以
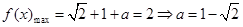 . 9分
. 9分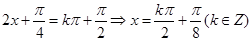 为
为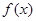 的对称轴. 12分
的对称轴. 12分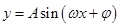 的图象与性质.
的图象与性质.
练习册系列答案
相关题目
 . 的部分图象如图所示,其中点
. 的部分图象如图所示,其中点 是图象的一个最高点.
是图象的一个最高点.
 的解析式;
的解析式; 且
且 ,求
,求 .
.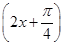 和函数y=cos
和函数y=cos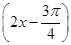 的图象关于原点对称;命题q:当x=kπ+
的图象关于原点对称;命题q:当x=kπ+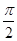 (k∈Z)时,函数y=
(k∈Z)时,函数y=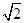 (sin 2x+cos 2x)取得极小值.下列说法正确的是( )
(sin 2x+cos 2x)取得极小值.下列说法正确的是( )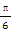 ),那么单摆来回摆动一次所需的时间为( )
),那么单摆来回摆动一次所需的时间为( )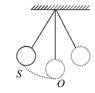
 图象的一条对称轴方程可以为( )
图象的一条对称轴方程可以为( )



 与函数g(x)=cos
与函数g(x)=cos ,下列说法正确的是( )
,下列说法正确的是( ) 对称
对称 (-2<x<10)的图像与x轴交于点A,过点A的直线l与函数的图像交于B,C两点,则(
(-2<x<10)的图像与x轴交于点A,过点A的直线l与函数的图像交于B,C两点,则( +
+ )·
)· =( )
=( )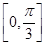 上单调递增,在区间
上单调递增,在区间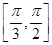 上单调递减,则ω=________.
上单调递减,则ω=________.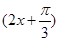 ,则下列结论正确的是( ).
,则下列结论正确的是( ).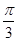 对称;②f(x)的图象关于点
对称;②f(x)的图象关于点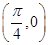 对称;③f(x)的图象向左平移
对称;③f(x)的图象向左平移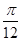 个单位,得到一个偶函数的图象;④f(x)的最小正周期为π,且在
个单位,得到一个偶函数的图象;④f(x)的最小正周期为π,且在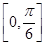 上为增函数
上为增函数