Question

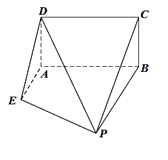
【题目】如图所示，正方体ABCD－A′B′C′D′的棱长为1，E，F分别是棱AA′，CC′的中点，过直线EF的平面分别与棱BB′、DD′分别交于M，N两点，设BM＝x，x∈[0,1]，给出以下四个结论：

①平面MENF⊥平面BDD′B′；

②直线AC∥平面MENF始终成立；

③四边形MENF周长L＝f(x)，x∈[0,1]是单调函数；

④四棱锥C′－MENF的体积V＝h(x)为常数；

以上结论正确的是__________．

Answer 1

【答案】①②④

【解析】连接，则，而，又平面， 平面， ，所以， ，由，所以平面 ， 平面，故平面 ，①正确；由前述证明可知平面， 平面，故平面，②也成立；四边形为菱形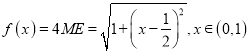， ，它不是单调函数，故③错； ， 到平面的距离为1， ，故为定值．故填①②④．