Question

【题目】如图，在△ABC中，∠ABC＝45°，点O在AB上，且OB＝OC＝AB，PO⊥平面ABC，DA∥PO，DA＝AO＝PO.

(1)求证：PB∥平面COD；

(2)求二面角O－CD－A的余弦值．

Answer 1

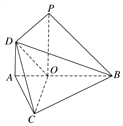
【答案】(1)见解析；(2)

【解析】试题分析：（1）利用平几知识计算可得OD∥PB，再根据线面平行判定定理得结论（2）过A作AM⊥DO，垂足为M，过M作MN⊥CD于N，则根据二面角定义得∠ANM为二面角O－CD－A的平面角．再解三角形可得二面角O－CD－A的余弦值．

试题解析：(1)证明　因为PO⊥平面ABC，DA∥PO，AB平面ABC，

所以PO⊥AB，DA⊥AB.

又DA＝AO＝PO，所以∠AOD＝45°.

因为OB＝AB，

所以OA＝AB，所以OA＝OB，

又AO＝PO，所以OB＝OP，

所以∠OBP＝45°，即OD∥PB.

又PB平面COD，OD平面COD，

所以PB∥平面COD.

(2)解　如图，过A作AM⊥DO，垂足为M，

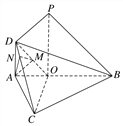
过M作MN⊥CD于N，连接AN，

则∠ANM为二面角O－CD－A的平面角．设AD＝a，

在等腰直角三角形AOD中，得AM＝a，

在直角三角形COD中，得MN＝a，

在直角三角形AMN中，得AN＝a，

所以cos∠ANM＝.