题目内容
已知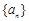 为等差数列,
为等差数列,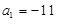 ,其前n项和为
,其前n项和为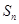 ,若
,若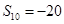 ,
,
(1)求数列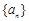 的通项;(2)求
的通项;(2)求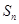 的最小值,并求出相应的
的最小值,并求出相应的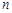 值.
值.
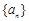 为等差数列,
为等差数列,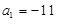 ,其前n项和为
,其前n项和为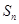 ,若
,若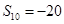 ,
,(1)求数列
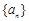 的通项;(2)求
的通项;(2)求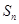 的最小值,并求出相应的
的最小值,并求出相应的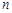 值.
值.(1) ,(2)
,(2) ,
, .
.
 ,(2)
,(2) ,
, .
.试题分析:(1)求等差数列通项,通法是待定系数法. 由
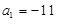 及
及 解得
解得 ,代入等差数列通项公式得:
,代入等差数列通项公式得: ,(2)研究等差数列前n项和最值,有两个思路,一是从
,(2)研究等差数列前n项和最值,有两个思路,一是从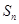 的表达式,即二次函数研究;二是从数列项的正负研究. 因为由题意得:,当
的表达式,即二次函数研究;二是从数列项的正负研究. 因为由题意得:,当 时
时 ,所以当
,所以当 时,
时,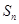 最小,因此
最小,因此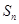 达到最小值的n等于6.
达到最小值的n等于6.试题解析:(1)由
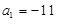 及
及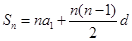 得
得 ,解得
,解得
所以

(2)令
 ,即
,即 得
得 。又
。又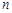 为正整数,
为正整数,所以当
 时
时 。
。所以当
 时,
时,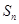 最小。
最小。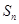 的最小值为
的最小值为
或者先求出
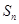 的表达式,再求它的最小值。
的表达式,再求它的最小值。
练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
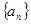 中,若
中,若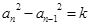 (
(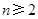 ,
,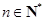 ,
,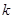 为常数),则称
为常数),则称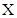 数列.
数列.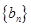 是
是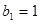 ,
,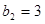 ,写出所有满足条件的数列
,写出所有满足条件的数列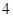 项;
项;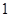 或
或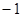 ;
;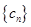 满足
满足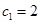 ,
,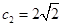 ,
,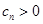 ,设数列
,设数列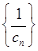 的前
的前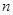 项和为
项和为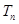 .是否存在
.是否存在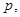
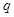 ,使不等式
,使不等式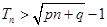 对一切
对一切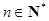 都成立?若存在,求出
都成立?若存在,求出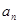 }的前n项和
}的前n项和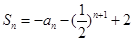 (n为正整数)。
(n为正整数)。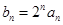 ,求证数列{
,求证数列{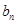 }是等差数列,并求数列{
}是等差数列,并求数列{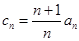 ,
,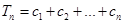 ,求
,求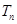 并证明:
并证明: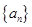 满足:
满足: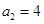 ,且对于任何
,且对于任何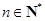 ,有
,有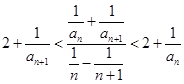 .
.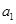 ,
,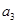 ;
;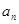 .
.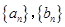 的前
的前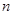 项和分别为
项和分别为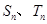 ,若
,若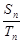 =
=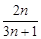 ,则
,则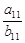 =_________
=_________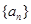 和
和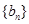 的前n项和分别为
的前n项和分别为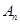 和
和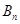 ,且
,且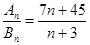 ,则使得
,则使得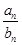 为整数的正整数n的个数是__________。
为整数的正整数n的个数是__________。 }中,
}中, =
= ,
, +
+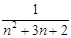 (n
(n ,则数列{
,则数列{

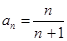

 满足:
满足: ,
, ,则
,则 ( )
( )


