题目内容
设正整数数列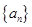 满足:
满足: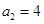 ,且对于任何
,且对于任何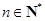 ,有
,有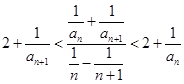 .
.
(1)求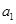 ,
,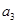 ;
;
(2)求数列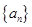 的通项
的通项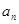 .
.
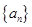 满足:
满足: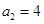 ,且对于任何
,且对于任何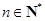 ,有
,有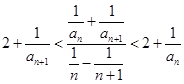 .
.(1)求
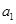 ,
,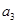 ;
;(2)求数列
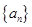 的通项
的通项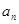 .
.(1) 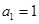 ,
,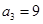 ;(2)
;(2)  .
.
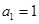 ,
,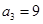 ;(2)
;(2)  .
.试题分析:(1)令
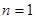 ,根据
,根据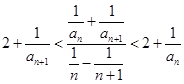 算得
算得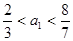 ,再根据
,再根据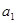 是正整数,算得.
是正整数,算得.当
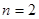 时,同样根据
时,同样根据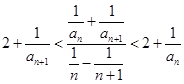 ,将
,将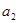 代入,得到
代入,得到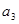 的范围,根据
的范围,根据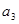 是正整数,求得
是正整数,求得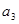 .
.(2)先根据
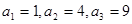 可猜想
可猜想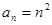 ,再用数学归纳法证明.
,再用数学归纳法证明.试题解析:解:(1)据条件得
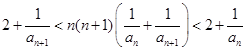 ①
①当
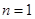 时,由
时,由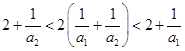 ,即有
,即有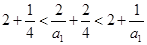 ,
,解得
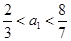 .因为
.因为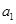 为正整数,故
为正整数,故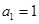 .
.当
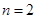 时,由
时,由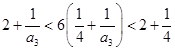 ,
,解得
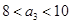 ,所以
,所以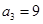 .
.(2)方法一:由
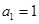 ,
,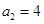 ,
,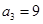 ,猜想:
,猜想: .
.下面用数学归纳法证明.
1
 当
当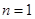 ,
,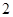 时,由(1)知
时,由(1)知 均成立;
均成立;2
 假设
假设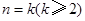 成立,则
成立,则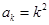 ,则
,则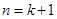 时
时由①得
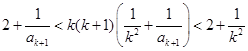
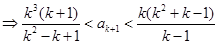
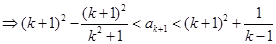
因为
 时,
时,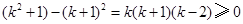 ,所以
,所以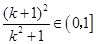 .
.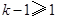 ,所以
,所以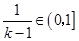 .
.又
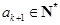 ,所以
,所以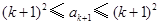 .
.故
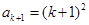 ,即
,即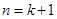 时,
时, 成立.
成立.由1
 ,2
,2 知,对任意
知,对任意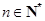 ,
, .
.(2)方法二:
由
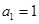 ,
,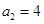 ,
,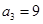 ,猜想:
,猜想: .
.下面用数学归纳法证明.
1
 当
当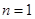 ,
,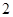 时,由(1)知
时,由(1)知 均成立;
均成立;2
 假设
假设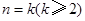 成立,则
成立,则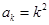 ,则
,则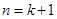 时
时由①得
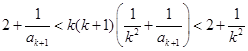
即
 ②
②由②左式,得
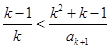 ,即
,即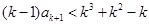 ,因为两端为整数,
,因为两端为整数,则
 .于是
.于是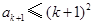 ③
③又由②右式,
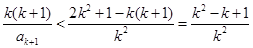 .
.则
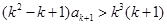 .
.因为两端为正整数,则
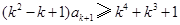 ,
,所以
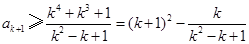 .
.又因
 时,
时,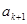 为正整数,则
为正整数,则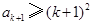 ④
④据③④
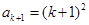 ,即
,即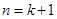 时,
时, 成立.
成立.由1
 ,2
,2 知,对任意
知,对任意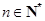 ,
, .
.
练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
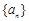 为等差数列,
为等差数列,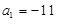 ,其前n项和为
,其前n项和为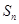 ,若
,若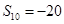 ,
,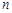 值.
值. .
.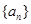 中,
中,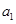 =1,
=1,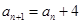 ,则
,则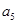 的值为____________.
的值为____________.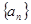 ,规定
,规定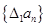 为数列
为数列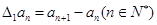 .
.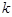 ,规定
,规定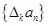 为
为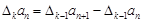 .若数列
.若数列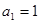 ,
,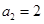 ,且满足
,且满足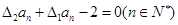 ,则
,则 .
. 中,若
中,若 ,则
,则 等于
等于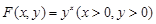 ,已知数列
,已知数列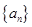 满足:
满足:
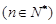 ,若对任意正整数
,若对任意正整数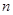 ,都有
,都有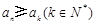 ,则
,则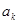 的值为
的值为  中,已知
中,已知 ,则
,则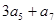 = ( )
= ( )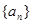 是等差数列,若
是等差数列,若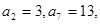 则数列
则数列