题目内容
5．水平放置棱长为2的正方体，以其各面中心为顶点的几何体的正、侧、俯视图的面积不可能为（ ）| A． | 4 | B． | 2 | C． | $\frac{{\sqrt{2}+\sqrt{6}}}{2}$ | D． | $\sqrt{2}$ |
分析 先判断正方体各个面的中心为顶点的凸多面体为正八面体，并画出图象、求出棱长和高，根据正方体和几何体的关系得到答案．
解答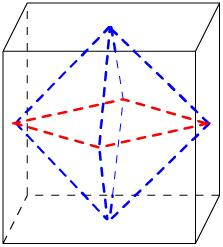 
解：正方体各个面的中心为顶点的凸多面体为正八面体，如图：
则棱长为a=$\sqrt{2}$，高为h=2，
∴八面体的正、侧、俯视图一定是原正方体各个面的一部分，
∴几何体的正、侧、俯视图的面积小于4，
故选：A．
点评 本题考查正方体的内接多面体，以及几何体的三视图，考查空间想象能力．
练习册系列答案
相关题目
15．已知函数$f（x）=\frac{{\sqrt{|x|}}}{e^x}（{x∈R}）$，若关于x的方程f2（x）-mf（x）+m-1=0恰好有4个不相等的实数根，则实数m的取值范围为（ ）
| A． | $（{1\;，\;\frac{{\sqrt{2e}}}{2e}+1}）$ | B． | $（{0\;，\;\frac{{\sqrt{2e}}}{2e}}）$ | C． | $（{1\;，\;\frac{1}{e}+1}）$ | D． | $（{\frac{{\sqrt{2e}}}{2e}\;，\;1}）$ |
13．已知f（x）=x3，若x∈[1，2]时，f（x2-ax）+f（1-x）≤0，则a的取值范围是（ ）
| A． | a≤1 | B． | a≥1 | C． | a≥$\frac{3}{2}$ | D． | a≤$\frac{3}{2}$ |
10．已知a＞0，函数f（x）=$\frac{|x-2a|}{x+2a}$在区间[1，4]上的最大值等于$\frac{1}{3}$，则a的值为（ ）
| A． | $\frac{1}{4}$ | B． | 1 | C． | 2 | D． | 4 |
15．已知抛物线C：y2=4x，O为坐标原点，F为其焦点，当点P在抛物线C上运动时，$\frac{|PO|}{|PF|}$的最大值为（ ）
| A． | $\frac{2\sqrt{3}}{3}$ | B． | $\frac{4}{3}$ | C． | $\frac{\sqrt{5}}{2}$ | D． | $\frac{5}{4}$ |
16．函数f（x）=3x+x-3的零点所在的区间是（ ）
| A． | （-2，-1） | B． | （-1，0） | C． | （0，1） | D． | （1，2） |