题目内容
函数y=f(x)为定义在R上的减函数,函数y=f(x-1)的图象关于点(1,0)对称,x,y满足不等式f(x2-2x)+f(2y-y2)≤0,M(1,2),N(x,y),O为坐标原点,则当1≤x≤4时, 的取值范围为________.
的取值范围为________.
 的取值范围为________.
的取值范围为________.[0,12]
因为函数y=f(x-1)的图象关于点(1,0)对称,
所以y=f(x)的图象关于原点对称,即函数y=f(x)为奇函数,
由f(x2-2x)+f(2y-y2)≤0得f(x2-2x)≤-f(2y-y2)=f(y2-2y),
所以x2-2x≥y2-2y,
所以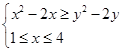 ,
,
即 ,
,
画出可行域如图,可得 =x+2y∈[0,12].
=x+2y∈[0,12].
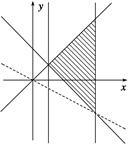
所以y=f(x)的图象关于原点对称,即函数y=f(x)为奇函数,
由f(x2-2x)+f(2y-y2)≤0得f(x2-2x)≤-f(2y-y2)=f(y2-2y),
所以x2-2x≥y2-2y,
所以
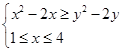 ,
,即
 ,
,画出可行域如图,可得
 =x+2y∈[0,12].
=x+2y∈[0,12].

练习册系列答案
相关题目
 的边长为1,则
的边长为1,则 .
.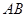 是半圆
是半圆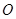 的直径,
的直径,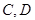 是弧
是弧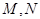 是线段
是线段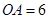 ,则
,则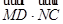 的值是( )
的值是( )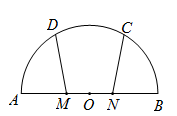




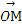 =(1,1),
=(1,1),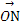 =(3,1),O为坐标原点,动点P(x,y)满足0≤
=(3,1),O为坐标原点,动点P(x,y)满足0≤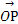 ·
·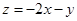 的最大值是 ( )
的最大值是 ( )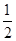
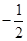
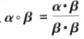 .若两个非零的平面向量
.若两个非零的平面向量 和
和 ,满足
,满足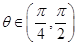 ,且
,且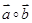 和
和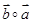 都在集合
都在集合 中,则
中,则


 ,向量
,向量 ,且
,且 ,那么
,那么 等于( )
等于( )



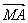 与
与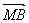 满足
满足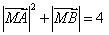 ,且
,且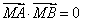 ,若点
,若点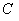 满足
满足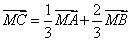 ,则
,则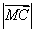 的最小值为( )
的最小值为( )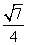
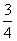
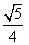
 ,
, 满足
满足 ,
, ,
, ,则
,则 ____.
____. 中,
中, ,则
,则 ____________.
____________.