题目内容
17.已知f(x)为偶函数,且f(x)在[0,+∞)单调递增,若f(ax+1)-f(x-2)≤0在$x∈[\frac{1}{2},1]$上恒成立,则实数a的取值范围是[-2,0].分析 因为偶函数在对称区间上单调性相反,根据已知中f(x)是偶函数,且f(x)在(0,+∞)上是增函数,易得f(x)在(-∞,0)上为减函数,又由若x∈[$\frac{1}{2}$,1]时,不等式f(ax+1)≤f(x-2)恒成立,结合函数恒成立的条件,求出x∈[$\frac{1}{2}$,1]时f(x-2)的最小值,从而可以构造一个关于a的不等式,解不等式即可得到实数a的取值范围.
解答 解:∵f(x)是偶函数,且f(x)在(0,+∞)上是增函数
∴f(x)在(-∞,0)上为减函数
当x∈[$\frac{1}{2}$,1]时,x-2∈[-$\frac{3}{2}$,-1]
故f(x-2)≥f(1)
若x∈[$\frac{1}{2}$,1]时,不等式f(ax+1)≤f(x-2)恒成立,
则当x∈[$\frac{1}{2}$,1]时,|ax+1|≤1恒成立,解得-2≤a≤0
故答案为[-2,0]
点评 本题的考点是函数恒成立问题,主要考查的知识点是奇偶性与单调性的综合,其中根据已知条件结合偶函数在对称区间上单调性相反,证得f(x)在(-∞,0)上为减函数,进而给出x∈[$\frac{1}{2}$,1]时f(x-2)的最小值,是解答本题的关键.

练习册系列答案
相关题目
8.幂函数f(x)的图象过点$({3,\root{3}{9}})$,则f(8)=( )
| A. | 8 | B. | 6 | C. | 4 | D. | 2 |
12.函数f(x)=$\frac{1}{{{3^x}-1}}$+a(x≠0),则“f(1)=1”是“函数f(x)为奇函数”的( )条件.
| A. | 充分不必要 | B. | 必要不充分 | ||
| C. | 充要 | D. | 既非充分又非必要 |
2.设集合A={x|1≤x≤6,x∈N},对于A的每个非空子集,定义其“交替和”如下:把集合中的数按从大到小的顺序排列,然后从最大的数开始交替地加减各数(如:{1,2,5}的“交替和”是5-2+1=4,{6,3}的“交替和”就是6-3=3,{3}的“交替和”就是3).则集合A的所有这些“交替和”的总和为( )
| A. | 128 | B. | 192 | C. | 224 | D. | 256 |
6.圆x2+y2-2x-5=0与圆x2+y2+2x-4y-4=0的交点为A,B,则线段AB的垂直平分线的方程是( )
| A. | x+y-1=0 | B. | 2x-y+1=0 | C. | x-2y+1=0 | D. | x-y+1=0 |
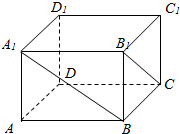 在长方体ABCD-A1B1C1D1中,已知DA=DC=4,DD1=3.
在长方体ABCD-A1B1C1D1中,已知DA=DC=4,DD1=3.