题目内容
【题目】已知F为抛物线![]()
![]() 的焦点,过F且倾斜角为
的焦点,过F且倾斜角为![]() 的直线交抛物线于A,B两点,
的直线交抛物线于A,B两点,![]() .
.
(1)求抛物线的方程:
(2)已知![]() 为抛物线上一点,M,N为抛物线上异于P的两点,且满足
为抛物线上一点,M,N为抛物线上异于P的两点,且满足![]() ,试探究直线MN是否过一定点?若是,求出此定点;若不是,说明理由.
,试探究直线MN是否过一定点?若是,求出此定点;若不是,说明理由.
【答案】(1)![]() (2)过定点,
(2)过定点,![]()
【解析】
(1)设出直线的方程,联立抛物线的方程,根据韦达定理即可求解出![]() 的值,即可求解出抛物线的方程;
的值,即可求解出抛物线的方程;
(2)求解出![]() 点坐标,设出直线
点坐标,设出直线![]() 的方程
的方程![]() ,根据
,根据![]() 求解出
求解出![]() 之间的关系,从而确定出直线所过的定点.
之间的关系,从而确定出直线所过的定点.
解:(1)由已知![]() ,直线AB的方程为
,直线AB的方程为![]()
联立直线与抛物线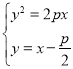 ,消y可得,
,消y可得,![]() ,所以
,所以![]() ,
,
因为![]()
![]()
![]() ,所以
,所以![]() ,
,
即抛物线的方程为![]() .
.
(2)将![]() 代入
代入![]() 可得
可得![]() ,
,
不妨设直线MN的方程为![]()
![]()
![]() ,
,
联立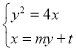 ,消x得
,消x得![]() ,
,
则有![]()
![]()
![]() ,
,
由题意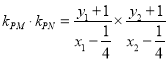
![]()
![]()
![]() ,
,
化简可得,![]() ,
,
代入![]()
![]()
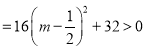
此时直线MN的方程为![]() ,
,
所以直线MN过定点![]() .
.

练习册系列答案
 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目