Question

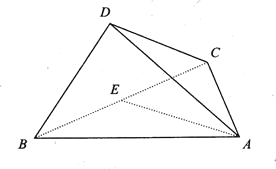
【题目】如图，已知梯形中，∥，，矩形平面，且,.

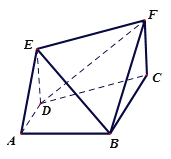
（1）求证：；

（2）求证：∥平面；

（3）求二面角的正切值.

Answer 1

【答案】(1)证明见解析；(2)证明见解析；(3)

【解析】

(1)根据面面垂直的性质定理证得平面,从而可得,再根据以及线面垂直的判定定理可得.平面,从而可得.

(3) 过点B作垂足为,作，垂足为,连接,则就是所求二面角的平面角,在三角形中,可求得答案.

解：（1）矩形平面，且平面平面=CD ,又平面.

平面.

又平面，

,

且,

.平面.

平面，

则

（2）如图所示:

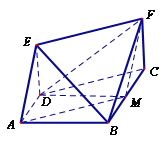
取中点M,连接,由已知条件易得及为平行四边形，于是,由于,故为平行四边形.

.面ABE,

所以 平面.又, 所以面,

又,所以平面平面. 又平面

∥平面.

（3）如图所示:

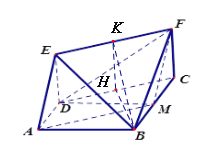
过点B作垂足为,作，垂足为,连接.由矩形平面，得平面,又,

所以就是所求二面角的平面角.

在△中,根据面积关系可得,得,得,解得.

在中， .

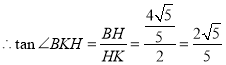故二面角的正切值为 .