题目内容
(本小题满分12分)
对于函数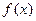 ,若存在
,若存在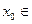 R,使
R,使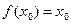 成立,则称
成立,则称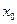 为
为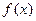 的不动点.如果函数
的不动点.如果函数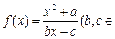 N*
N*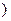 有且仅有两个不动点0和2,且
有且仅有两个不动点0和2,且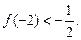
(1)求实数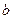 ,
,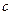 的值;
的值;
(2)已知各项不为零的数列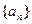
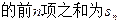 ,并且
,并且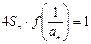 , 求数列
, 求数列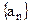 的通项公式;;
的通项公式;;
(3)求证: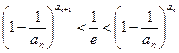 .
.
对于函数
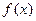 ,若存在
,若存在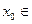 R,使
R,使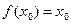 成立,则称
成立,则称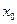 为
为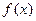 的不动点.如果函数
的不动点.如果函数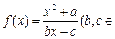 N*
N*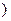 有且仅有两个不动点0和2,且
有且仅有两个不动点0和2,且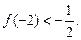
(1)求实数
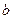 ,
,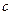 的值;
的值;(2)已知各项不为零的数列
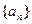
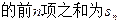 ,并且
,并且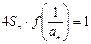 , 求数列
, 求数列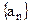 的通项公式;;
的通项公式;;(3)求证:
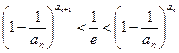 .
.(1)c="2 " b=2
(2)
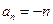 (
(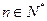 )
)(3)略
(1)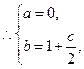
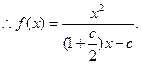
由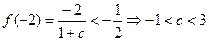 ,又
,又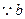 ,
,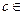 N*,
N*,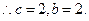 ……(3分)
……(3分)
(2)由(1)知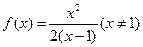 ,
,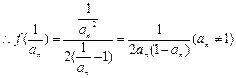 ,
,
又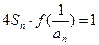 ,
,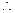
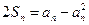 ,当
,当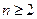 时,
时,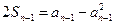 ,
,
两式相减,得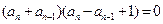 ,
,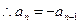 或
或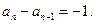 )
)
当
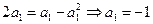 ,若
,若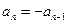 ,则
,则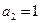 ,这与
,这与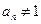 矛盾.
矛盾.
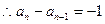 ,
,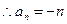 .(
.(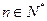 ) ……………(6分)
) ……………(6分)
(3)由(2)知,待证不等式即为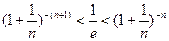 ,
,
它等价于 两边取对数可得
两边取对数可得
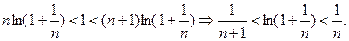 ………………(8分)
………………(8分)
若令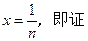
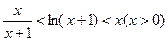 ,
,
构造函数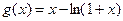 ,
,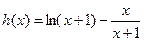 ,
,
则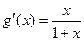 ,
,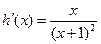 ,
,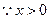 ,
,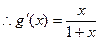 ,
,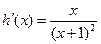 .
.
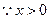 ,
,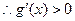 ,
,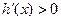 ,
,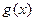 、
、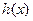 在
在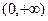 上都是增函数,
上都是增函数,
于是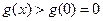 ,
,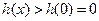 ,从而当
,从而当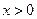 时,
时,
则有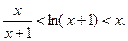 即
即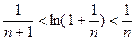 ,
,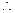 原不等式成立. ……(12分)
原不等式成立. ……(12分)
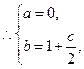
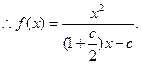
由
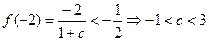 ,又
,又 ,
,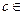 N*,
N*,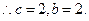 ……(3分)
……(3分)(2)由(1)知
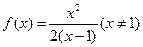 ,
,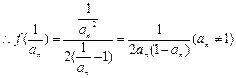 ,
,又
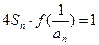 ,
,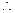
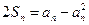 ,当
,当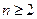 时,
时,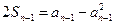 ,
,两式相减,得
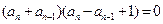 ,
,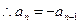 或
或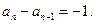 )
)当

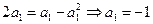 ,若
,若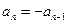 ,则
,则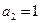 ,这与
,这与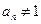 矛盾.
矛盾. 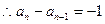 ,
,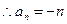 .(
.(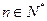 ) ……………(6分)
) ……………(6分)(3)由(2)知,待证不等式即为
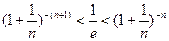 ,
,它等价于
 两边取对数可得
两边取对数可得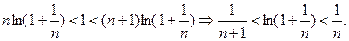 ………………(8分)
………………(8分)若令
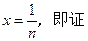
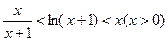 ,
,构造函数
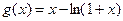 ,
,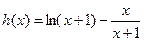 ,
,则
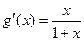 ,
,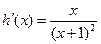 ,
,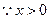 ,
,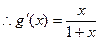 ,
,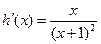 .
.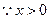 ,
,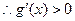 ,
,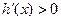 ,
,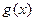 、
、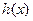 在
在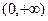 上都是增函数,
上都是增函数,于是
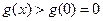 ,
,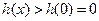 ,从而当
,从而当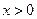 时,
时,则有
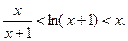 即
即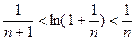 ,
,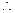 原不等式成立. ……(12分)
原不等式成立. ……(12分)
练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
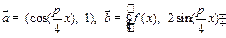 ,
,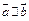 . 数列
. 数列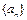 满足
满足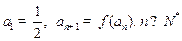 .
.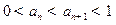 ;
;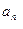 ≥
≥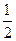 ,证明:
,证明: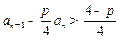 ;
;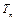 是数列
是数列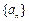 的前
的前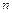 项和,判断
项和,判断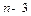 的大小,并说明理由.
的大小,并说明理由.  有且只有两个不动点0,2,且
有且只有两个不动点0,2,且
 (
( 为
为 数列前n项和),求数列通项
数列前n项和),求数列通项 ;
; ,求证:当
,求证:当 时,恒有
时,恒有 成立.
成立.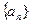 是等差数列,
是等差数列,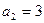 ,
,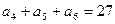 ,
,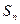 为数列
为数列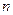 项和
项和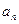 和
和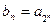 ,求数列
,求数列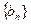 的前
的前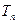
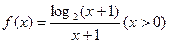 上有一点列
上有一点列 ,点
,点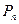 在x轴上的射影是
在x轴上的射影是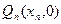 ,且
,且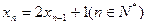 ,
,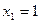 .
.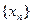 的通项公式;
的通项公式;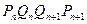 的面积是
的面积是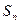 ,求证:
,求证: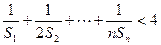
 是首项为1的等差数列,且
是首项为1的等差数列,且 ,若
,若 成等比数列,(1)求数列
成等比数列,(1)求数列 ,求数列
,求数列 的前
的前 项和
项和 .
.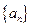 中,
中,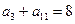 ,数列
,数列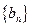 是等比数列,且
是等比数列,且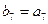 ,则
,则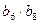 的值为( )
的值为( )
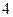
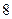

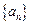 的前n项和为
的前n项和为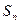 ,若
,若 ,点A(3,
,点A(3,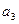 )与B(5,
)与B(5,  )都在斜率为-2的直线
)都在斜率为-2的直线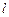 上,则使
上,则使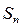 取得最大值的
取得最大值的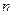 值为( )
值为( )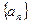 中,若
中,若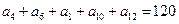 ,则
,则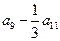 的值为 ( )
的值为 ( )