题目内容
4.为了整顿食品的安全卫生,食品监督部门对某食品厂生产的甲、乙两种食品进行了检测调研,检测某种有害微量元素的含量,随机在两种食品中各抽取了10个批次的食品,每个批次各随机地抽取了一件,卞表是测量数据的茎叶图(单位:毫克)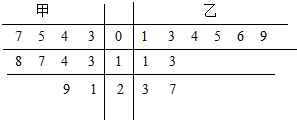
规定:当食品中的有害微量元素含量在[0,10]时为一等品,在(10,20]为二等品,20以上为劣质品.
(1)分别求出甲、乙两种食品该有害微量元素含量的样本平均数,并据此判定哪种食品的质量较好;
(2)若用分层抽样的方法,分别在两组数据中各抽取5个数据,分别求出甲、乙两种食品一等品的件数;
(3)在(2)的条件下,从甲组5个数据中随机抽取2个,求恰有一件一等品的概率.
分析 (1)根据平均数的定义,计算得到两组数据的平均数,即可判定哪种食品的质量较好;
(2)依据分层抽样的方法,即可得到求出甲、乙两种食品一等品的件数;
(3)列出从甲组5个数据中随机抽取2个,所有可能的结果,然后找出恰有一件一等品的结果,根据古典概型的概率公式解之即可.
解答 解:(1)根据平均数的定义,
则${\overline{x}}_{甲}$=$\frac{1}{10}$(3+4+5+7+13+14+17+18+21+29)=13.1,
${\overline{x}}_{乙}$=$\frac{1}{10}$(1+3+4+5+6+9+11+13+23+27)=10.2,
由于${\overline{x}}_{甲}$>${\overline{x}}_{乙}$,故乙种食品的质量较好;
(2)甲种食品一等品的件数为4×$\frac{5}{10}$=2件,
乙种食品一等品的件数为6×$\frac{5}{10}$=3件;
(3)设甲组中的两件一等品为A,B,非一等品为c,d,e,
则从这5个数据中随机抽取2个,所有可能的结果为:
AB,Ac,Ad,Ae,Bc,Bd,Be,cd,ce,de,共10种,
其中恰有一件一等品的情况有6种,
故恰有一件一等品的概率为P=$\frac{6}{10}=\frac{3}{5}$.
点评 本题主要考查了茎叶图,平均数以及利用列举法计算基本事件及其发生的概率,同时考查了运算求解的能力,属于基础题.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
14.已知实数a,b,c满足不等式0<a<b<c<1,且M=2a,N=5-b,P=($\frac{1}{7}$)c,则M、N、P的大小关系为( )
| A. | M>N>P | B. | P<M<N | C. | N>P>M |
12.已知集合A={x|-1≤x≤1},B={x|x2-2x≤0},则A∩B=( )
| A. | [-1,0] | B. | [-1,2] | C. | [0,1] | D. | (-∞,1]∪[2,+∞) |
19.设函数f(x)=sin(2x+φ)(0<φ<$\frac{π}{2}$)的图象的一条对称轴是直线x=$\frac{π}{8}$,则f(x)的单调递增区间是( )
| A. | (-$\frac{3π}{8}+kπ,\frac{π}{8}+kπ$)k∈Z | B. | (-$\frac{3π}{8}+\frac{kπ}{2},\frac{π}{8}+\frac{kπ}{2}$)k∈Z | ||
| C. | ($\frac{π}{8}+kπ,\frac{5π}{8}+kπ$)k∈Z | D. | (-$\frac{3π}{8}+2kπ,\frac{π}{8}+2kπ$)k∈Z |
9.设复数z满足(z+2i)(2+i)=5,则z=( )
| A. | 3-2i | B. | 3+2i | C. | 2-3i | D. | 2+3i |
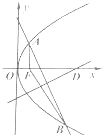 抛物线y2=4x的焦点为F,过点(0,3)的直线与抛物线交于A,B两点,线段AB的垂直平分线交x轴于点D,若|AF|+|BF|=6,则点D的横坐标为4.
抛物线y2=4x的焦点为F,过点(0,3)的直线与抛物线交于A,B两点,线段AB的垂直平分线交x轴于点D,若|AF|+|BF|=6,则点D的横坐标为4.