题目内容
【题目】给出下列说法:
①命题“若![]() ,则
,则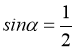 ”的否命题是假命题;
”的否命题是假命题;
②命题![]() ,使
,使![]() ,则
,则![]() ;
;
③“![]() ”是“函数
”是“函数![]() 为偶函数”的充要条件;
为偶函数”的充要条件;
④命题![]() “
“![]() ,使
,使![]() ”,命题
”,命题![]() “在
“在![]() 中,若
中,若![]() ,则
,则![]() ”,那么命题
”,那么命题![]() 为真命题.
为真命题.
其中正确的个数是( )
A.1B.2C.3D.4
【答案】C
【解析】
写出否命题,举反例判断①;根据否定的定义判断②;根据充分条件以及必要条件的定义以及正弦函数的性质证明即可判断③;由三角函数的性质判断![]() 为假命题,根据正弦定理判断
为假命题,根据正弦定理判断![]() 为真命题,即可得出
为真命题,即可得出![]() 为真命题.
为真命题.
①项,命题“若![]() ,则
,则 ”的否命题为“若
”的否命题为“若![]() ,则
,则![]() ”
”
因为![]() ,所以否命题是假命题,①项正确;
,所以否命题是假命题,①项正确;
②项,命题![]() ,使
,使![]() ,含有一个量词的否定在否定结论的同时,要改变量词的属性,存在量词改为全称量词,则
,含有一个量词的否定在否定结论的同时,要改变量词的属性,存在量词改为全称量词,则![]() ,②项正确;
,②项正确;
③项,充分性:当![]() 时,函数
时,函数![]() 为偶函数,充分性成立;
为偶函数,充分性成立;
必要性:若函数![]() 为偶函数,则
为偶函数,则![]() ,可得
,可得![]() ,必要性不成立,③项错误;
,必要性不成立,③项错误;
④项,命题![]() “
“![]() ,使
,使![]() ”
”
因为![]() ,所以当
,所以当![]() 时,
时,![]() ,即命题
,即命题![]() 为假命题;
为假命题;
命题![]() “在
“在![]() 中,若
中,若![]() ,则
,则![]() ”,根据正弦定理可知
”,根据正弦定理可知
![]() ,则
,则![]() ,即
,即![]() ,所以
,所以![]() 为真命题,则命题
为真命题,则命题![]() 为真命题,④项正确.
为真命题,④项正确.
故选:C

【题目】某地有种特产水果很受当地老百姓欢迎,但该种水果只能在9月份销售,且该种水果只能当天食用口感最好,隔天食用口感较差。某超市每年9月份都销售该特产水果,每天计划进货量相同,进货成本每公斤8元,销售价每公斤12元;当天未卖出的水果则转卖给水果罐头厂,但每公斤只能卖到5元。根据往年销售经验,每天需求量与当地气温范围有一定关系。如果气温不低于30度,需求量为5000公斤;如果气温位于![]() ,需求量为3500公斤;如果气温低于25度,需求量为2000公斤;为了制定今年9月份订购计划,统计了前三年9月份的气温范围数据,得下面的频数分布表
,需求量为3500公斤;如果气温低于25度,需求量为2000公斤;为了制定今年9月份订购计划,统计了前三年9月份的气温范围数据,得下面的频数分布表
气温范围 |
|
|
|
|
|
天数 | 4 | 14 | 36 | 21 | 15 |
以气温范围位于各区间的频率代替气温范围位于该区间的概率.
(1)求今年9月份这种水果一天需求量![]() (单位:公斤)的分布列和数学期望;
(单位:公斤)的分布列和数学期望;
(2)设9月份一天销售特产水果的利润为![]() (单位:元),当9月份这种水果一天的进货量为
(单位:元),当9月份这种水果一天的进货量为![]() (单位:公斤)为多少时,
(单位:公斤)为多少时,![]() 的数学期望达到最大值,最大值为多少?
的数学期望达到最大值,最大值为多少?