Question

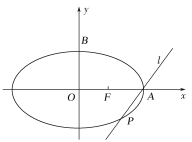
【题目】过函数的图象上一点作倾斜角互补的两条直线，分别与交与异于的，两点.

（1）求证：直线的斜率为定值；

（2）如果，两点的横坐标均不大于0，求面积的最大值.

Answer 1

【答案】（1）见解析；（2）6

【解析】

（1）由题意易知直线的斜率存在且不为0，则可表示出的直线方程，与联立求得的坐标，同理可得的坐标，进而求得的斜率；

（2）设出直线的方程与联立消去，利用判别式大于0求得的范围，进而表示出三角形的面积为，利用换元法令，利用导数判断单调性确定面积的最大值.

（1）由题意易知直线的斜率存在且不为0，

可设直线方程为，即，

由于两直线倾斜角互补，故直线的方程为，

设，，

由得，

∵，即，则，

即，同理可得，

∴的斜率为，

即直线的斜率为定值.

（2）设直线的方程为，

由得，

由得，

又A、B的横坐标不大于零，

∴，，则，

，

于是，点到直线的距离，

则的面积，

令，，，

∴，

令，，

求导可得在上恒成立，

∴在上单调递增，则最大值为，

故面积的最大值为6.