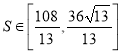题目内容
【题目】已知函数![]() 的图象在点
的图象在点![]() 处的切线斜率为
处的切线斜率为![]() ,其中
,其中![]() 为自然对数的底数.
为自然对数的底数.
(1)求实数![]() 的值,并求
的值,并求![]() 的单调区间;
的单调区间;
(2)证明:![]() .
.
【答案】(1)![]() ,函数的单调递减区间
,函数的单调递减区间![]() ,函数单调递增区间
,函数单调递增区间![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
(1)先对函数求导,然后结合导数的几何意义可求![]() ,结合导数与单调性关系即可求解.
,结合导数与单调性关系即可求解.
(2)要证明原不等式成立,可转化为证明求解相应函数的范围,进行合理的变形后构造函数,结合导数可证.
解:(1)函数![]() 的定义域为
的定义域为![]() .
.![]() ,由题意可得,
,由题意可得,![]() e,故a
e,故a![]() ,
,![]() .
.
当![]() 时,
时,![]() ,函数
,函数![]() 单调递减,当
单调递减,当![]() 时,
时,![]() ,函数
,函数![]() 单调递增,故函数
单调递增,故函数![]() 的单调递减区间为
的单调递减区间为![]() ,单调递增区间为
,单调递增区间为![]() .
.
(2)证明:设![]() ,则
,则![]() .
.
当x![]() 时,
时,![]() ,函数
,函数![]() 单调递减,当x
单调递减,当x![]() 时,
时,![]() ,函数
,函数![]() 单调递增,故
单调递增,故![]() .
.
设![]() ,则
,则![]() ,当
,当![]() 时,
时,![]() ,函数
,函数![]() 单调递增,当
单调递增,当![]() 时,
时,![]() ,函数
,函数![]() 单调递减,故
单调递减,故![]() .
.
综上可得,![]() 时,恒有
时,恒有![]() ,即
,即![]() .
.

 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案【题目】为了提高生产线的运行效率,工厂对生产线的设备进行了技术改造.为了对比技术改造后的效果,采集了生产线的技术改造前后各20次连续正常运行的时间长度(单位:天)数据,并绘制了如下茎叶图:
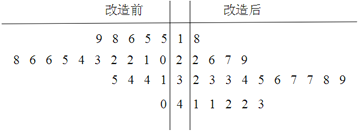
(Ⅰ)(1)设所采集的40个连续正常运行时间的中位数![]() ,并将连续正常运行时间超过
,并将连续正常运行时间超过![]() 和不超过
和不超过![]() 的次数填入下面的列联表:
的次数填入下面的列联表:
超过 | 不超过 | |
改造前 |
|
|
改造后 |
|
|
试写出![]() ,
,![]() ,
,![]() ,
,![]() 的值;
的值;
(2)根据(1)中的列联表,能否有![]() 的把握认为生产线技术改造前后的连续正常运行时间有差异?
的把握认为生产线技术改造前后的连续正常运行时间有差异?
附: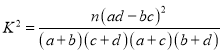 ,
,
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
(Ⅱ)工厂的生产线的运行需要进行维护.工厂对生产线的生产维护费用包括正常维护费、保障维护费两种对生产线设定维护周期为![]() 天(即从开工运行到第
天(即从开工运行到第![]() 天(
天(![]() )进行维护.生产线在一个生产周期内设置几个维护周期,每个维护周期相互独立.在一个维护周期内,若生产线能连续运行,则不会产生保障维护费;若生产线不能连续运行,则产生保障维护费.经测算,正常维护费为0.5万元
)进行维护.生产线在一个生产周期内设置几个维护周期,每个维护周期相互独立.在一个维护周期内,若生产线能连续运行,则不会产生保障维护费;若生产线不能连续运行,则产生保障维护费.经测算,正常维护费为0.5万元![]() 次;保障维护费第一次为0.2万元
次;保障维护费第一次为0.2万元![]() 周期,此后每增加一次则保障维护费增加0.2万元.现制定生产线一个生产周期(以120天计)内的维护方案:
周期,此后每增加一次则保障维护费增加0.2万元.现制定生产线一个生产周期(以120天计)内的维护方案:![]() ,
,![]() ,2,3,4.以生产线在技术改造后一个维护周期内能连续正常运行的频率作为概率,求一个生产周期内生产维护费的分布列及期望值.
,2,3,4.以生产线在技术改造后一个维护周期内能连续正常运行的频率作为概率,求一个生产周期内生产维护费的分布列及期望值.
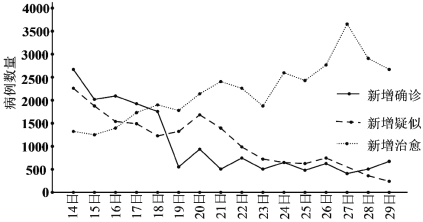
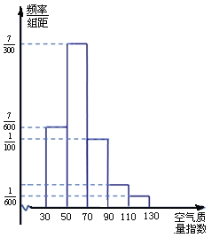
【题目】某市积极贯彻落实国务院《“十三五”节能减排综合工作方案》,空气质量明显改善.该市生态环境局统计了某月(30天)空气质量指数,绘制成如下频率分布直方图.已知空气质量等级与空气质量指数对照如下表:
空气质量指数 |
|
|
|
|
| 300以上 |
空气质量等级 | 一级 (优) | 二级 (良) | 三级 (轻度污染) | 四级 (中度污染) | 五级 (重度污染) | 六级 (严重污染) |
(1)根据频率分布直方图估计,在这30天中,空气质量等级为优或良的天数;
(2)根据体质检查情况,医生建议:当空气质量指数高于90时,市民甲不宜进行户外体育运动;当空气质量指数高于70时,市民乙不宜进行户外体育运动(两人是否进行户外体育运动互不影响).
①从这30天中随机选取2天,记乙不宜进行户外体育运动,且甲适宜进行户外体育运动的天数为X,求X的分布列和数学期望;
②以该月空气质量指数分布的频率作为以后每天空气质量指数分布的概率(假定每天空气质量指数互不影响),甲、乙两人后面分别随机选择3天和2天进行户外体育运动,求甲恰有2天,且乙恰有1天不宜进行户外体育运动的概率.