Question

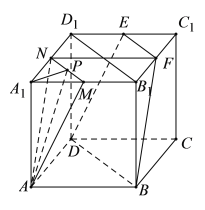
【题目】在棱长为1的正方体ABCD﹣A1B1C1D1中，点E，F分别是棱C1D1，B1C1的中点，P是上底面A1B1C1D1内一点，若AP∥平面BDEF，则线段AP长度的取值范围是（ ）

A.[，]B.[，]C.[，]D.[，]

Answer 1

【答案】B

【解析】

分别取棱A1B1、A1D1的中点M、N，连接MN，可证平面AMN∥平面BDEF，得P点在线段MN上．由此可判断当P在MN的中点时，AP最小；当P与M或N重合时，AP最大．然后求解直角三角形得答案．

如图所示，分别取棱A1B1、A1D1的中点M、N，连接MN，连接B1D1，

∵M、N、E、F为所在棱的中点，∴MN∥B1D1，EF∥B1D1，

∴MN∥EF，又MN平面BDEF，EF平面BDEF，∴MN∥平面BDEF；

连接NF，由NF∥A1B1，NF＝A1B1，A1B1∥AB，A1B1＝AB，

可得NF∥AB，NF＝AB，则四边形ANFB为平行四边形，

则AN∥FB，而AN平面BDEF，FB平面BDEF，则AN∥平面BDEF．

又AN∩NM＝N，∴平面AMN∥平面BDEF．

又P是上底面A1B1C1D1内一点，且AP∥平面BDEF，∴P点在线段MN上．

在Rt△AA1M中，AM，

同理，在Rt△AA1N中，求得AN，则△AMN为等腰三角形．

当P在MN的中点时，AP最小为，

当P与M或N重合时，AP最大为．

∴线段AP长度的取值范围是[，]．

故选：B．