题目内容
(本小题12分)已知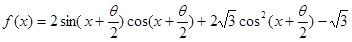
(Ⅰ)若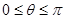 ,求
,求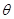 使函数
使函数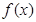 为偶函数。
为偶函数。
(Ⅱ)在(I)成立的条件下,求满足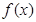 =1,
=1, ∈[-π,π]的
∈[-π,π]的 的集合。
的集合。
(1) (2)-
(2)- 或
或
解析试题分析:解:(1) f (x)=sin(2x+θ)+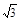 cos(2x+θ)
cos(2x+θ)
=2sin(2x+θ+ )……………………4分
)……………………4分
要使f (x)为偶函数,则必有f (-x)=f (x)
∴ 2sin(-2x+θ+ )=2sin (2x+θ+
)=2sin (2x+θ+ )
)
∴ 2sin2x cos(θ+ )=0对x∈R恒成立
)=0对x∈R恒成立
∴ cos(θ+ )=0又0≤θ≤π θ=
)=0又0≤θ≤π θ= ……………………7分
……………………7分
(2) 当θ= 时f (x)=2sin(2x+
时f (x)=2sin(2x+ )=2cos2x=1
)=2cos2x=1
∴cos2x= ∵x∈[-π,π] ∴x=-
∵x∈[-π,π] ∴x=- 或
或 ………………12分
………………12分
考点:本试题考查了三角函数函数的图像性质。
点评:解决该试题的关键是利用偶函数的定义,得到参数的方程,进而得到参数的值,同时能利用对称轴处函数值为最值,进而求解得到x的取值集合,属于中档题。

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
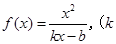 ,
,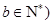 ,满足
,满足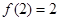 ,
,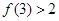 .
.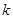 ,
,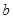 的值;
的值;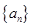 的前
的前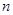 项和为
项和为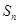 ,且有
,且有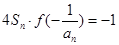 ,设
,设 ,求数列
,求数列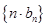 的前
的前 ;
;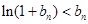 .
.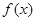 满足
满足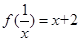 .
.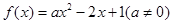 .
.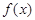 有两个零点,求
有两个零点,求 的取值范围;
的取值范围;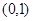 与
与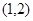 上各有一个零点,求
上各有一个零点,求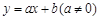 ,
,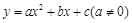 ,
,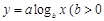 且
且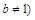 ,请你根据表中的数据,选取一个恰当的函数,使它能合理描述产品利润Q与销量t的变化,求所选取的函数的解析式,并求利润最大时的销量.
,请你根据表中的数据,选取一个恰当的函数,使它能合理描述产品利润Q与销量t的变化,求所选取的函数的解析式,并求利润最大时的销量. 分)已知函数
分)已知函数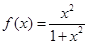 .
.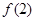 与
与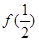 ,
,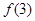 与
与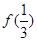 ;
; 与
与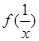 有什么关系?并证明你的结论;
有什么关系?并证明你的结论;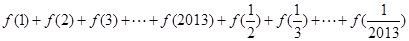 的值 .
的值 .