题目内容
(本小题满分14分)
已知函数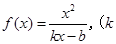 ,
,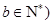 ,满足
,满足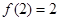 ,
,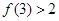 .
.
(1)求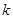 ,
,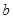 的值;
的值;
(2)若各项为正的数列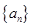 的前
的前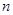 项和为
项和为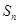 ,且有
,且有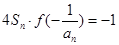 ,设
,设 ,求数列
,求数列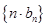 的前
的前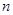 项和
项和 ;
;
(3)在(2)的条件下,证明: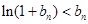 .
.
(1)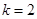 ,
,
(2)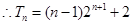
(3)通过构造函数,利用导数的思想来分析函数单调性,进而得到证明。
解析试题分析:解:(1)由 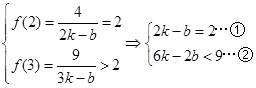 ,
,
由 代入
代入 可得
可得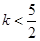 ,且
,且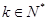 .……………………………………………………2分
.……………………………………………………2分
当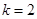 时,
时,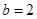 (成立),当
(成立),当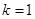 时,
时,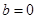 (舍去).
(舍去).
所以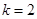 ,
,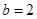 .…………………………………………………………………………4分
.…………………………………………………………………………4分
(2)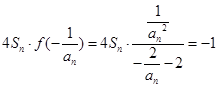 ,即
,即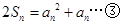 .
.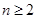 时,
时, 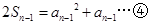 .
.
所以,当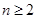 时,由
时,由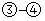 可得
可得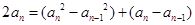 ,
,
整理得,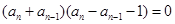 .
.
又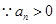 得
得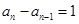 ,且
,且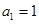 ,
,
所以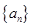 是首项为1,公差为1的等差数列,即
是首项为1,公差为1的等差数列,即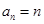 ,
,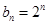 .
.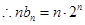 . ………………………………………………………………………………7分
. ………………………………………………………………………………7分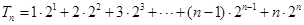 ,
,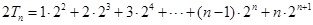 ,
,
由上两式相减得 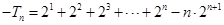
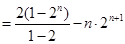 .
.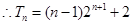 . ……………………………………………………………………10分
. ……………………………………………………………………10分
(3)由(2)知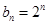 ,只需证
,只需证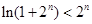 .设
.设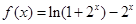 (
(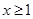 且
且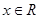 ).
).
则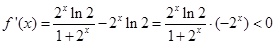 ,
,
可知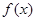 在
在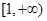 上是递减,
上是递减,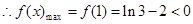 .
.
由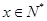 ,则
,则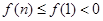 ,
,
故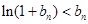 . …………………………………………………………………………14分
. …………………………………………………………………………14分
考点:数列的通项公式与前n项和的运用。
点评:解决数列与函数与不等式的综合试题,是高考中常考的知识交汇点试题,熟练掌握错位相减法求和,属于中档题。

练习册系列答案
相关题目
 有三个极值点。
有三个极值点。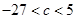 ;
;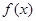 在区间
在区间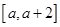 上单调递减,求
上单调递减,求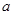 的取值范围。
的取值范围。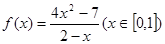
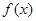 的单调区间和值域。
的单调区间和值域。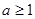 ,求函数
,求函数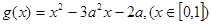 ,若对于任意
,若对于任意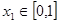 ,总存在
,总存在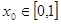 ,使得
,使得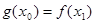 成立,求实数
成立,求实数 的取值范围。
的取值范围。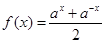 (
(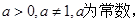 x∈R).
x∈R).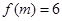 ,求
,求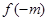 的值;
的值;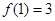 ,求
,求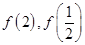 的值。
的值。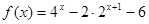 ,其中
,其中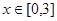 。
。 的最大值和最小值;
的最大值和最小值;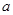 满足:
满足: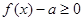 恒成立,求
恒成立,求
 时,求
时,求 的单调区间;
的单调区间; ,
,  恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.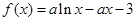 (a∈R且
(a∈R且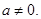 ).
). 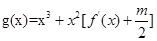 在区间(t,3)上总不是单调函数,求m的取值范围.
在区间(t,3)上总不是单调函数,求m的取值范围.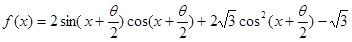
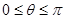 ,求
,求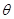 使函数
使函数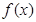 为偶函数。
为偶函数。 ∈[-π,π]的
∈[-π,π]的