题目内容
(Ⅰ) ;(Ⅱ)
;(Ⅱ) 。
。
解析试题分析:(Ⅰ)由已知可得 ,
, , 2分
, 2分
所以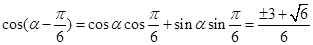 . 4分
. 4分
(Ⅱ)
= . 6分
. 6分
因为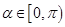 ,则
,则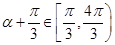 ,所以
,所以 ,
,
故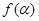 的值域是
的值域是 . 8分
. 8分
考点:三角函数线;和差公式;
点评:求三角函数的值域,一般用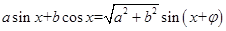 化为
化为 的形式,然后根据三角函数的单调性来求。
的形式,然后根据三角函数的单调性来求。

练习册系列答案
相关题目
题目内容
(Ⅰ) ;(Ⅱ)
;(Ⅱ) 。
。
解析试题分析:(Ⅰ)由已知可得 ,
, , 2分
, 2分
所以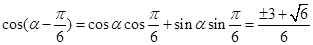 . 4分
. 4分
(Ⅱ)
= . 6分
. 6分
因为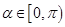 ,则
,则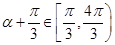 ,所以
,所以 ,
,
故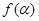 的值域是
的值域是 . 8分
. 8分
考点:三角函数线;和差公式;
点评:求三角函数的值域,一般用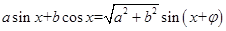 化为
化为 的形式,然后根据三角函数的单调性来求。
的形式,然后根据三角函数的单调性来求。
