题目内容
【题目】已知函数f(x)= ![]() 的定义域为(﹣1,1),满足f(﹣x)=﹣f(x),且f(
的定义域为(﹣1,1),满足f(﹣x)=﹣f(x),且f( ![]() )=
)= ![]() .
.
(1)求函数f(x)的解析式;
(2)证明f(x)在(﹣1,1)上是增函数;
(3)解不等式f(x2﹣1)+f(x)<0.
【答案】
(1)解:由题意知,f(x)为奇函数;
∴f(0)=b=0,则 ![]() ;
;
又 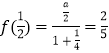 ;
;
∴a=1;
∴ ![]()
(2)解:设﹣1<x1<x2<1,则:
![]() =
= ![]() ;
;
又﹣1<x1<x2<1;
∴ ![]() ;
;
∴f(x1)﹣f(x2)<0;
即f(x1)<f(x2);
∴f(x)在(﹣1,1)上是增函数;
(3)解:由f(x2﹣1)+f(x)<0得f(x2﹣1)<﹣f(x);
即f(x2﹣1)<f(﹣x);
由(2)知f(x)在(﹣1,1)上是增函数,则 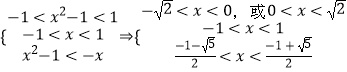
![]() ;
;
∴原不等式的解集为 ![]()
【解析】(1)根据条件即可得出f(x)为奇函数,原点有定义,从而f(0)=0,得出b=0,再由f( ![]() )=
)= ![]() 即可求出a=1;(2)根据增函数的定义,设任意的﹣1<x1<x2<1,然后作差,通分,证明f(x1)<f(x2),从而便得出f(x)在(﹣1,1)上是增函数;(3)根据f(x)为奇函数便可得出f(x2﹣1)<﹣f(x),由f(x)在(﹣1,1)上为增函数即可得到不等式组
即可求出a=1;(2)根据增函数的定义,设任意的﹣1<x1<x2<1,然后作差,通分,证明f(x1)<f(x2),从而便得出f(x)在(﹣1,1)上是增函数;(3)根据f(x)为奇函数便可得出f(x2﹣1)<﹣f(x),由f(x)在(﹣1,1)上为增函数即可得到不等式组 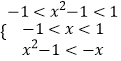 ,解该不等式组便可得出原不等式的解集.
,解该不等式组便可得出原不等式的解集.

练习册系列答案
相关题目