题目内容
(本题满分14分)
在数列{an}中,已知,a1=2,an+1+ an+1 an=2 an.对于任意正整数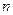 ,
,
(1)求数列{an}的通项an的表达式;
(2)若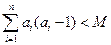 (
(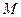 为常数,且为整数),求
为常数,且为整数),求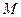 的最小值.
的最小值.
在数列{an}中,已知,a1=2,an+1+ an+1 an=2 an.对于任意正整数
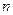 ,
,(1)求数列{an}的通项an的表达式;
(2)若
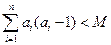 (
(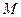 为常数,且为整数),求
为常数,且为整数),求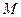 的最小值.
的最小值. (1)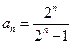
(2) M的最小值为3
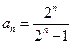
(2) M的最小值为3
解:(Ⅰ)由题意,对于n∈N*,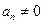 ,且
,且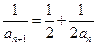 ,即
,即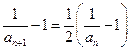 .
.
由 ,得
,得 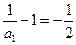 .则数列
.则数列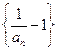 是首项为
是首项为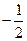 ,公比为
,公比为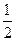 的等比数列.于是
的等比数列.于是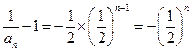 , 即
, 即 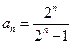 . ………6分
. ………6分
(Ⅱ)由(Ⅰ),得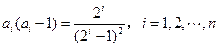 . 当
. 当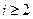 时,因为
时,因为
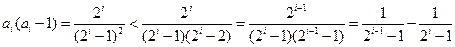 ,
,
所以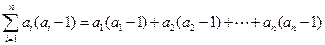
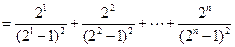
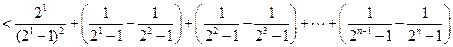
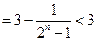 .
.
又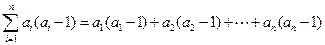
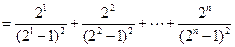
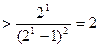 ,故M的最小值为3.………14分
,故M的最小值为3.………14分
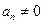 ,且
,且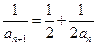 ,即
,即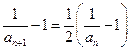 .
.由
 ,得
,得 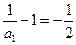 .则数列
.则数列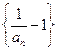 是首项为
是首项为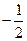 ,公比为
,公比为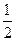 的等比数列.于是
的等比数列.于是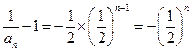 , 即
, 即 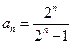 . ………6分
. ………6分 (Ⅱ)由(Ⅰ),得
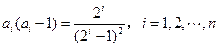 . 当
. 当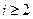 时,因为
时,因为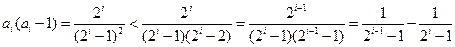 ,
, 所以
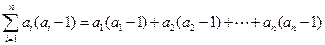
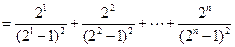
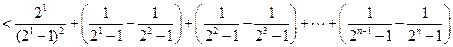
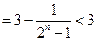 .
.又
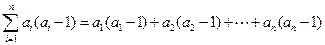
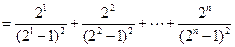
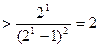 ,故M的最小值为3.………14分
,故M的最小值为3.………14分
练习册系列答案
相关题目
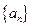 ,且
,且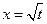 是函数
是函数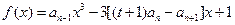 ,(
,(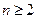 )的一个极值点.数列
)的一个极值点.数列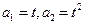 (
(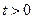 且
且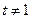 ).
).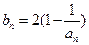 ,当
,当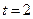 时,数列
时,数列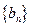 的前
的前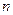 项
项 和为
和为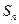 ,求使
,求使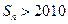 的
的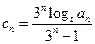 ,证明:
,证明: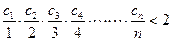 (
(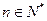 )。
)。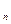 }满足S
}满足S
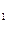 、a
、a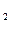 、a
、a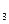 、a
、a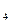 ,并由此猜想通项公式a
,并由此猜想通项公式a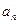 }中
}中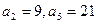 .
.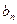 =
=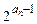 ,求数列
,求数列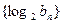 的前
的前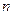 项和
项和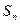 .
.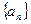 中,
中,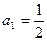 ,点
,点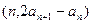 在直线
在直线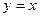 上,其中
上,其中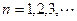
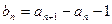 ,求证:数列
,求证:数列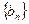 是等比数列;
是等比数列;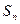 、
、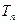 分别为数列
分别为数列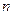 项和,是否存在实数
项和,是否存在实数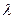 使得数列
使得数列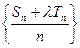 为等差数列?若存在,试求出
为等差数列?若存在,试求出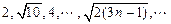 ,那么10是这个数列的第 ▲ 项.
,那么10是这个数列的第 ▲ 项.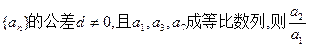 =" " ( )
=" " ( )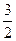
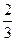
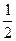
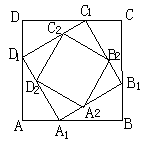 如图,在边长为
如图,在边长为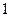 的正方形ABCD中的四条边上有A1、B1、C1、D1四点,分别把AB、BC、CD、DA分成1:2,得到一个小正方形A1B1C1D1,再用同样的方法在正方形A1B1C1D1内做正方形A2B2C2D2,…,这样无限的做下去,则所有这些正方形面积之和为 .
的正方形ABCD中的四条边上有A1、B1、C1、D1四点,分别把AB、BC、CD、DA分成1:2,得到一个小正方形A1B1C1D1,再用同样的方法在正方形A1B1C1D1内做正方形A2B2C2D2,…,这样无限的做下去,则所有这些正方形面积之和为 .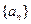 是公差为正数的等差数列,
是公差为正数的等差数列,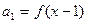 ,
,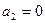 ,
,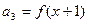 ,其中
,其中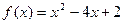 ,则数列
,则数列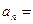 ______________
______________