题目内容
.数列{a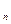 }满足S
}满足S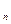 = 2n-a
= 2n-a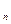 , n∈N
, n∈N
⑴计算a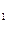 、a
、a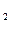 、a
、a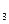 、a
、a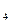 ,并由此猜想通项公式a
,并由此猜想通项公式a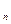
(2)用数字归纳法证明(1)中的猜想.
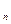 }满足S
}满足S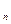 = 2n-a
= 2n-a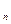 , n∈N
, n∈N
⑴计算a
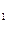 、a
、a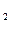 、a
、a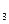 、a
、a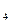 ,并由此猜想通项公式a
,并由此猜想通项公式a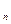
(2)用数字归纳法证明(1)中的猜想.
(1)a =
=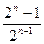 ( n∈N
( n∈N )
)
(2)略
 =
=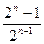 ( n∈N
( n∈N )
)(2)略
解: (1) a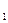 =1、a
=1、a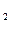 =
=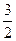 、a
、a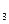 =
=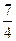 、a
、a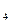 =
=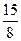
猜想a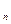 =
=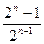 ( n∈N
( n∈N )
)
证明:①当n = 1时,a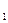 = 1结论成立
= 1结论成立
②假设n =" K" (K≥1)时,结论成立
即a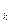 =
=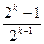 , 那么n=k+1时
, 那么n=k+1时
a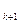 =S
=S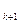 -S
-S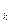 ="2(k+1)" -a
="2(k+1)" -a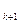 -2k+
-2k+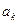
=2+a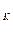 -a
-a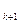
∴2 a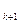 ="2+" a
="2+" a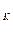
∴a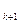 =
=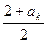 =
=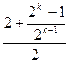 =
=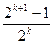
这表明n=k+1时,结论成立
∴a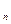 =
=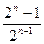
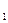 =1、a
=1、a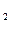 =
=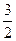 、a
、a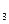 =
=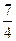 、a
、a =
=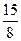
猜想a
 =
=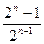 ( n∈N
( n∈N )
)证明:①当n = 1时,a
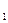 = 1结论成立
= 1结论成立②假设n =" K" (K≥1)时,结论成立
即a
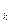 =
=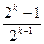 , 那么n=k+1时
, 那么n=k+1时a
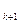 =S
=S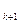 -S
-S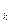 ="2(k+1)" -a
="2(k+1)" -a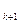 -2k+
-2k+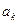
=2+a
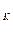 -a
-a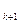
∴2 a
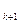 ="2+" a
="2+" a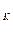
∴a
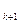 =
=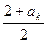 =
=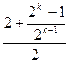 =
=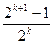
这表明n=k+1时,结论成立
∴a
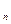 =
=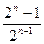

练习册系列答案
相关题目
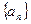 中
中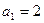 ,点
,点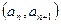 在函数
在函数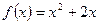 的图象上,
的图象上,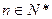 .数列
.数列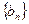 的前n项和为
的前n项和为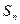 ,且满足
,且满足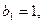 当
当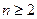 时,
时,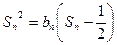
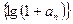 是等比数列;
是等比数列;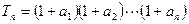 ,
,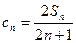 ,求
,求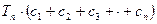 的值.
的值.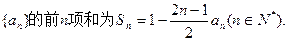
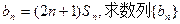 的通项公式;
的通项公式;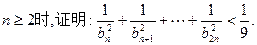
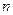 ,
,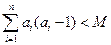 (
(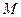 为常数,且为整数),求
为常数,且为整数),求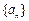 的前n项和为
的前n项和为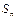 ,其中
,其中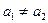 .
.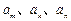 是数列
是数列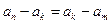 的任意项.
的任意项.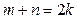 ;
;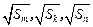 也成等差数列,且
也成等差数列,且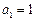 ,求数列
,求数列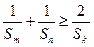 .
.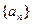 满足
满足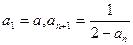 (n≥1)(
(n≥1)(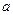 ≠2)
≠2)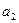 ,
,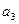 ,
,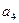 ;
;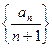 的前n项和为 。
的前n项和为 。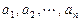 满足
满足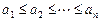 ,则
,则 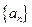 的前
的前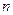 项和为
项和为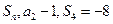 .
.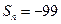 ,求
,求