题目内容
10.已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1(a>b>0)$的左,右焦点分别为F1,F2,右顶点为A,椭圆上的点M满足MF1⊥x轴,MA的中点为N,直线NF2的斜率k=-$\frac{5}{9}$.(1)求椭圆C的离心率;
(2)若直线NF1交椭圆于H,K两点,且|HK|=$\frac{50}{3}$,求椭圆C的方程.
分析 (1)F1(-c,0),F2(c,0),A(a,0).把x=-c代入椭圆方程可取M$(-c,\frac{{b}^{2}}{a})$,N$(\frac{a-c}{2},\frac{{b}^{2}}{2a})$.利用斜率计算公式可得:9c2+15ac-14a2=0,4=0,解出即可.
(2)由e=$\frac{2}{3}$,可得$a=\frac{3}{2}c$,N$(\frac{c}{4},\frac{5}{12}c)$,利用斜率计算公式可得${k}_{{F}_{1}N}$=$\frac{1}{3}$,直线NF1的方程为:$y=\frac{1}{3}(x+c)$.与椭圆方程联立化为24x2+8cx-41c2=0,利用根与系数的关系可得:|HK|=$\sqrt{(1+\frac{1}{9})[({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}]}$,解得c.即可得出.
解答 解:(1)F1(-c,0),F2(c,0),A(a,0).
把x=-c代入椭圆方程可得:$\frac{{c}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$,解得y=$±\frac{{b}^{2}}{a}$,取M$(-c,\frac{{b}^{2}}{a})$,
∴N$(\frac{a-c}{2},\frac{{b}^{2}}{2a})$.
∴直线NF2的斜率k=-$\frac{5}{9}$=$\frac{\frac{{b}^{2}}{2a}-0}{\frac{a-c}{2}-c}$,化为9c2+15ac-14a2=0,
∴9e2+15e-14=0.0<e<1.
解得e=$\frac{2}{3}$.
(2)∵e=$\frac{2}{3}$,∴$a=\frac{3}{2}c$,∴N$(\frac{c}{4},\frac{5}{12}c)$,
∴${k}_{{F}_{1}N}$=$\frac{\frac{5}{12}c-0}{\frac{c}{4}-(-c)}$=$\frac{1}{3}$,
∴直线NF1的方程为:$y=\frac{1}{3}(x+c)$.
联立$\left\{\begin{array}{l}{y=\frac{1}{3}(x+c)}\\{\frac{4{x}^{2}}{9{c}^{2}}+\frac{4{y}^{2}}{5{c}^{2}}=1}\end{array}\right.$,
化为24x2+8cx-41c2=0,∴x1+x2=-$\frac{1}{3}c$,x1x2=$-\frac{41{c}^{2}}{24}$.
∴|HK|=$\sqrt{(1+\frac{1}{9})[({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}]}$=$\sqrt{\frac{10}{9}×(\frac{{c}^{2}}{9}+4×\frac{41{c}^{2}}{24})}$=$\frac{50}{3}$,
化为c2=36,解得c=6.
∴椭圆C的方程为:$\frac{{x}^{2}}{81}+\frac{{y}^{2}}{45}$=1.
点评 本题考查了椭圆的标准方程及其性质、直线与椭圆相交弦长问题、一元二次方程的根与系数的关系、斜率计算公式,考查了推理能力与计算能力,属于难题.

| A. | (3,2) | B. | (-3,2) | C. | (-3,-2) | D. | (-2,3) |
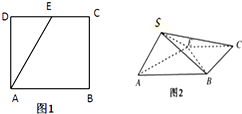 如图,点E为正方形ABCD边CD上异于点C,D的动点,将△ADE沿AE翻折成△SAE,使得平面SAE⊥平面ABCE,则下列三个说法中正确的个数是( )
如图,点E为正方形ABCD边CD上异于点C,D的动点,将△ADE沿AE翻折成△SAE,使得平面SAE⊥平面ABCE,则下列三个说法中正确的个数是( )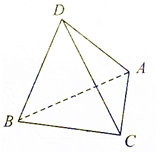 如图,A、B、C、D为空间四点,△ABC中,AB=AC=BC=2,等边三角形ADB以AB为轴运动,当平面ADB⊥平面ABC时,则CD=$\sqrt{6}$.
如图,A、B、C、D为空间四点,△ABC中,AB=AC=BC=2,等边三角形ADB以AB为轴运动,当平面ADB⊥平面ABC时,则CD=$\sqrt{6}$.