题目内容
已知圆 满足:
满足:
①截y轴所得弦长为2;
②被x轴分成两段圆弧,其弧长的比为 .
.
求在满足条件①②的所有圆中,使代数式 取得最小值时,圆的方程.
取得最小值时,圆的方程.
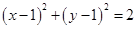 ,或
,或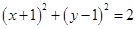
解析试题分析:由①②,根据直线与圆相交时,半径、半弦与弦心距的关系,得到参数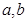 的关系式,从而可把代数式
的关系式,从而可把代数式 化成关于
化成关于 或
或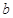 的一元二次函数,求出这个二次函数的最值及取得最值时相对应的
的一元二次函数,求出这个二次函数的最值及取得最值时相对应的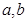 的值,最后确定圆的方程.
的值,最后确定圆的方程.
试题解析:如下图所示,圆心坐标为P(a,b),半径为r,则点P到x轴,y轴的距离分别为|b|,|a|.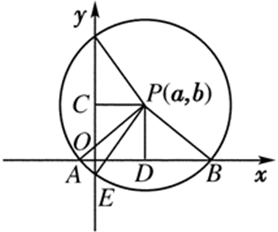
∵圆P被x轴分成两段圆弧,其弧长的比为3:1,
∴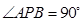 .
.
取AB的中点D,连接PD,
则有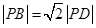 ,∴
,∴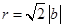 .
.
取圆P截y轴的弦的中点C,连接PC,PE.
∵圆截y轴所得弦长为2,
∴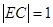 ,∴
,∴ ,
,
即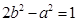 .
.
则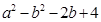 =
=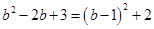 .
.
∴当b=1时,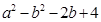 取得最小值2,
取得最小值2,
此时a=1,或a=-1,r2=2.
对应的圆为: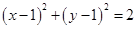 ,
,
或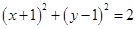 .
.
∴使代数式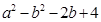 取得最小值时,对应的圆为
取得最小值时,对应的圆为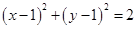 ,或
,或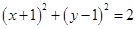 .
.
考点:1、圆的标准方程;2、直线与圆的位置关系;3、一元二次函数的最值.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 的方程为
的方程为 ,直线
,直线
 ,设点
,设点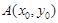 .
. 在圆
在圆 与圆
与圆 ,
, ,过点
,过点 分别交圆
分别交圆 两点,且直线
两点,且直线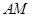 和
和 的斜率互为相反数;
的斜率互为相反数;  的值;
的值;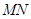 的斜率是否为定值?若是,求出该定值;若不是,说明理由.
的斜率是否为定值?若是,求出该定值;若不是,说明理由. 上,求圆C的方程。
上,求圆C的方程。 与已知圆
与已知圆 的交点,且在两坐标轴上的四个截距之和为8的圆的方程。
的交点,且在两坐标轴上的四个截距之和为8的圆的方程。 ,设点
,设点 是直线
是直线 上的两点,它们的横坐标分别是
上的两点,它们的横坐标分别是 ,点
,点 在线段
在线段 上,过
上,过 的切线
的切线 ,切点为
,切点为 .
. ,求直线
,求直线 三点的圆的圆心是
三点的圆的圆心是 ,求线段
,求线段 (
( 为坐标原点)长的最小值
为坐标原点)长的最小值 .
. .
. 过点
过点 ,且与圆
,且与圆 相切,求直线
相切,求直线 的半径为4,圆心
的半径为4,圆心 :
: 上,且与圆
上,且与圆