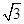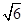题目内容
已知抛物线 上存在关于直线
上存在关于直线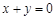 对称的相异两点A、B,则|AB|等于
对称的相异两点A、B,则|AB|等于
A. 3 B. 4 C.  D.
D. 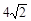
C
解析试题分析:因为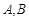 关于直线
关于直线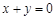 对称,所以
对称,所以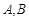 在与
在与 平行的直线上,因此
平行的直线上,因此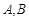 为直线
为直线 与抛物线
与抛物线 的交点,且线段
的交点,且线段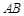 的中点在直线
的中点在直线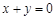 上.由方程
上.由方程 得中点横坐标
得中点横坐标 ,所以纵坐标为
,所以纵坐标为 ,因此
,因此

考点:对称点的求法

练习册系列答案
相关题目
抛物线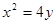 上一点
上一点 的纵坐标为4,则点
的纵坐标为4,则点 与抛物线焦点的距离为( )
与抛物线焦点的距离为( )
| A.2 | B.3 | C.4 | D.5 |
若双曲线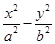 =1(a>0,b>0)与直线y=
=1(a>0,b>0)与直线y=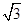 x无交点,则离心率e的取值范围是( ).
x无交点,则离心率e的取值范围是( ).
| A.(1,2) | B.(1,2] | C.(1, ) ) | D.(1, ] ] |
O为坐标原点,F为抛物线C:y2=4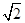 x的焦点,P为C上一点,若|PF|=4
x的焦点,P为C上一点,若|PF|=4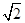 ,则△POF的面积为( ).
,则△POF的面积为( ).
| A.2 | B.2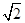 | C.2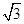 | D.4 |
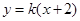 与双曲线
与双曲线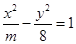 ,有如下信息:联立方程组:
,有如下信息:联立方程组: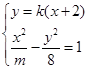 , 消去
, 消去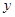 后得到方程
后得到方程 ,分类讨论:(1)当
,分类讨论:(1)当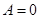 时,该方程恒有一解;(2)当
时,该方程恒有一解;(2)当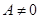 时,
时,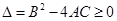 恒成立。在满足所提供信息的前提下,双曲线离心率的取值范围是
恒成立。在满足所提供信息的前提下,双曲线离心率的取值范围是 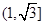
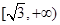
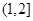
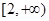
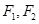 分别是椭圆为
分别是椭圆为 :
:
 的左、右焦点,过点
的左、右焦点,过点 作
作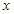 轴的垂线交椭圆
轴的垂线交椭圆 ,过点
,过点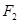 作直线
作直线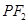 的垂线交直线
的垂线交直线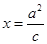 于点
于点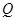 ,若直线
,若直线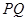 与双曲线
与双曲线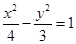 的一条渐近线平行,则椭圆的离心率为( )
的一条渐近线平行,则椭圆的离心率为( )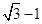
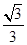


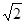
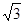
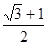
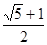
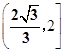
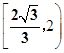
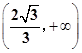
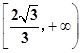
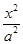 -y2=1(a>0)交于A,B两点,点F为抛物线的焦点,若△FAB为直角三角形,则双曲线的离心率是( ).
-y2=1(a>0)交于A,B两点,点F为抛物线的焦点,若△FAB为直角三角形,则双曲线的离心率是( ).