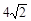题目内容
已知直线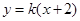 与双曲线
与双曲线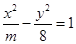 ,有如下信息:联立方程组:
,有如下信息:联立方程组: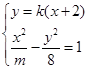 , 消去
, 消去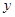 后得到方程
后得到方程 ,分类讨论:(1)当
,分类讨论:(1)当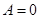 时,该方程恒有一解;(2)当
时,该方程恒有一解;(2)当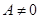 时,
时,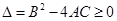 恒成立。在满足所提供信息的前提下,双曲线离心率的取值范围是
恒成立。在满足所提供信息的前提下,双曲线离心率的取值范围是
A.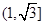 | B.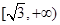 |
C.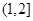 | D.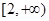 |
B
解析试题分析:联立方程组: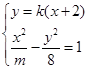 , 消去
, 消去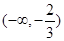 后得到方程
后得到方程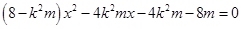 ,此时
,此时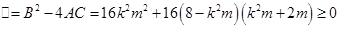 恒成立,即
恒成立,即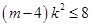 恒成立,解得
恒成立,解得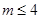 ;所以双曲线离心率
;所以双曲线离心率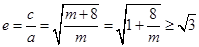 ,即
,即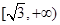 为正确答案.
为正确答案.
考点:新定义问题、双曲线离心率的求法.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
椭圆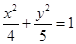 的一个焦点坐标是( )
的一个焦点坐标是( )
A.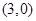 | B.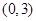 | C.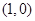 | D.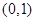 |
双曲线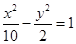 的焦距为
的焦距为
A.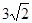 | B.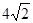 | C.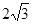 | D.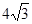 |
抛物线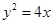 的焦点坐标为( )
的焦点坐标为( )
| A.(2,0) | B.(1,0) | C.(0,-4) | D.(-2,0) |
已知椭圆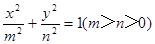 和双曲线
和双曲线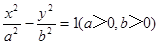 有相同的焦点
有相同的焦点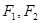 ,
, 是两曲线的一个交点,则
是两曲线的一个交点,则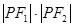 的值是( )
的值是( )
A.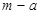 | B. | C.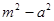 | D. |
已知双曲线 =1(a>0,b>0)的一个焦点与抛物线y2=4
=1(a>0,b>0)的一个焦点与抛物线y2=4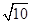 x的焦点重合,且双曲线的离心率等于
x的焦点重合,且双曲线的离心率等于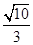 ,则该双曲线的方程为( )
,则该双曲线的方程为( )
A.x2-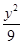 =1 =1 | B.x2-y2=15 | C.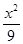 -y2=1 -y2=1 | D.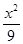 - -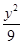 =1 =1 |
若抛物线y2=2px的焦点与双曲线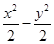 =1的右焦点重合,则p的值为( )
=1的右焦点重合,则p的值为( )
| A.-2 | B.2 | C.-4 | D.4 |
已知双曲线C: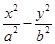 =1(a>0,b>0)的离心率为
=1(a>0,b>0)的离心率为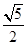 ,则C的渐近线方程为( ).
,则C的渐近线方程为( ).
A.y=±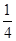 x x | B.y=±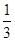 x x |
C.y=± x x | D.y=±x |
 上存在关于直线
上存在关于直线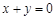 对称的相异两点A、B,则|AB|等于
对称的相异两点A、B,则|AB|等于  D.
D.