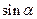题目内容
已知函数 (
(
 R).
R).
(1) 当 时,求函数
时,求函数 的极值;
的极值;
(2)若函数 的图象与
的图象与 轴有且只有一个交点,求a的取值范围.
轴有且只有一个交点,求a的取值范围.
 (
(
 R).
R).(1) 当
 时,求函数
时,求函数 的极值;
的极值;(2)若函数
 的图象与
的图象与 轴有且只有一个交点,求a的取值范围.
轴有且只有一个交点,求a的取值范围.(Ⅰ)当 时,
时,  取得极大值为
取得极大值为
 ;当
;当 时,
时,  取得极小值为-6.(Ⅱ)a的取值范围是
取得极小值为-6.(Ⅱ)a的取值范围是 .
.
 时,
时,  取得极大值为
取得极大值为
 ;当
;当 时,
时,  取得极小值为-6.(Ⅱ)a的取值范围是
取得极小值为-6.(Ⅱ)a的取值范围是 .
.(1)当 时,
时, ,
,
∴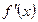
 .
.
令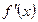 ="0," 得
="0," 得 . …… 2分
. …… 2分
当 时,
时, , 则
, 则 在
在 上单调递增;
上单调递增;
当 时,
时, , 则
, 则 在
在 上单调递减;
上单调递减;
当 时,
时, ,
,  在
在 上单调递增.
上单调递增.
∴当 时,
时,  取得极大值为
取得极大值为
 ;
;
当 时,
时,  取得极小值为
取得极小值为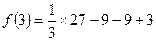
 . …… 5分
. …… 5分
(2) ∵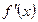 =
=  ,
,
∴△= =
=  .
.
①若a≥1,则△≤0, …… 6分
∴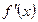 ≥0在R上恒成立,
≥0在R上恒成立,
∴f(x)在R上单调递增 .
∵f(0)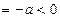 ,
, ,
,
∴当a≥1时,函数f(x)的图象与x轴有且只有一个交点. …… 8分
②若a<1,则△>0,
∴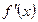 = 0有两个不相等的实数根,不妨设为x1,x2,(x1<x2).
= 0有两个不相等的实数根,不妨设为x1,x2,(x1<x2).
∴x1+x2 = 2,x1x2 = a.
当 变化时,
变化时, 的取值情况如下表:
的取值情况如下表:
…… 9分
∵ ,
,
∴ .
.
∴



 .
.
同理
 .
.
∴


 .
.
令f(x1)·f(x2)>0, 解得a> .
.
而当 时,
时, ,
,
故当 时,函数f(x)的图象与x轴有且只有一个交点. …… 11分
时,函数f(x)的图象与x轴有且只有一个交点. …… 11分
综上所述,a的取值范围是 . …… 12分
. …… 12分
 时,
时, ,
,∴
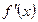
 .
. 令
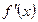 ="0," 得
="0," 得 . …… 2分
. …… 2分 当
 时,
时, , 则
, 则 在
在 上单调递增;
上单调递增;当
 时,
时, , 则
, 则 在
在 上单调递减;
上单调递减;当
 时,
时, ,
,  在
在 上单调递增.
上单调递增. ∴当
 时,
时,  取得极大值为
取得极大值为
 ;
;当
 时,
时,  取得极小值为
取得极小值为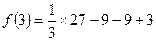
 . …… 5分
. …… 5分(2) ∵
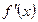 =
=  ,
,∴△=
 =
=  .
. ①若a≥1,则△≤0, …… 6分
∴
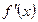 ≥0在R上恒成立,
≥0在R上恒成立,∴f(x)在R上单调递增 .
∵f(0)
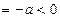 ,
, ,
, ∴当a≥1时,函数f(x)的图象与x轴有且只有一个交点. …… 8分
②若a<1,则△>0,
∴
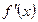 = 0有两个不相等的实数根,不妨设为x1,x2,(x1<x2).
= 0有两个不相等的实数根,不妨设为x1,x2,(x1<x2).∴x1+x2 = 2,x1x2 = a.
当
 变化时,
变化时, 的取值情况如下表:
的取值情况如下表: | x | 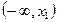 | x1 | (x1,x2) | x2 |  |
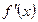 | + | 0 | - | 0 | + |
| f(x) | ↗ | 极大值 | ↘ | 极小值 | ↗ |
∵
 ,
,∴
 .
.∴




 .
.同理

 .
.∴



 .
.令f(x1)·f(x2)>0, 解得a>
 .
. 而当
 时,
时, ,
,故当
 时,函数f(x)的图象与x轴有且只有一个交点. …… 11分
时,函数f(x)的图象与x轴有且只有一个交点. …… 11分 综上所述,a的取值范围是
 . …… 12分
. …… 12分
练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案
相关题目
 是定义在
是定义在 上的奇函数,当
上的奇函数,当 时,
时,  (其中e是自然界对数的底,
(其中e是自然界对数的底, )(1)求
)(1)求 ,求证:当
,求证:当 时,
时, ;(3)是否存在实数a,使得当
;(3)是否存在实数a,使得当 时,
时, ,其中
,其中 .(1)若
.(1)若 ,求
,求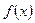 的单调递增区间;(2)如果函数
的单调递增区间;(2)如果函数 的取值范围;(3)求证对任意的
的取值范围;(3)求证对任意的 ,不等式
,不等式 恒成立
恒成立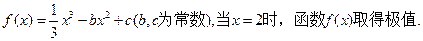
 的单调区间;(Ⅱ)若函数
的单调区间;(Ⅱ)若函数

 且
且 ,求函数
,求函数 的极大值与极小值.
的极大值与极小值. 的单调递增区间是 ( )
的单调递增区间是 ( )

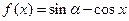 ,则
,则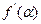 等于( )
等于( )