题目内容
(本小题满分13分)设函数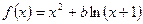 ,其中
,其中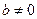 .(1)若
.(1)若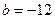 ,求
,求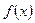 的单调递增区间;(2)如果函数
的单调递增区间;(2)如果函数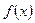 在定义域内既有极大值又有极小值,求实数
在定义域内既有极大值又有极小值,求实数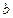 的取值范围;(3)求证对任意的
的取值范围;(3)求证对任意的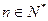 ,不等式
,不等式 恒成立
恒成立
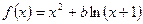 ,其中
,其中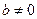 .(1)若
.(1)若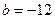 ,求
,求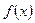 的单调递增区间;(2)如果函数
的单调递增区间;(2)如果函数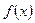 在定义域内既有极大值又有极小值,求实数
在定义域内既有极大值又有极小值,求实数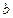 的取值范围;(3)求证对任意的
的取值范围;(3)求证对任意的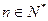 ,不等式
,不等式 恒成立
恒成立(Ⅰ) 当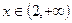 时,
时,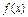 单调递增 (Ⅱ)
单调递增 (Ⅱ) 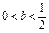 (Ⅲ)略
(Ⅲ)略
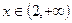 时,
时,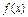 单调递增 (Ⅱ)
单调递增 (Ⅱ) 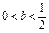 (Ⅲ)略
(Ⅲ)略(1)由题意知,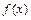 的定义域为
的定义域为 ,
,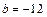 时,由
时,由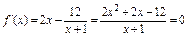 ,得
,得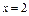 (
(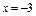 舍去),当x
舍去),当x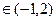 时,
时,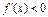 ,当
,当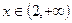 时,
时,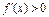 ,所以当
,所以当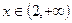 时,
时,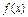 单调递增。
单调递增。
(2)由题意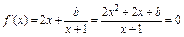 在
在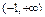 有两个不等实根,即
有两个不等实根,即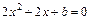 在
在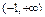 有两个不等实根,设
有两个不等实根,设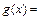
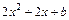 ,则
,则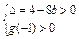 ,解之得
,解之得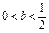
(3)对于函数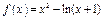 ,令函数
,令函数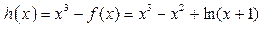
则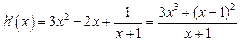 ,
,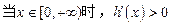 ,所以函数
,所以函数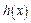 在
在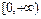 上单调递增,又
上单调递增,又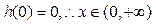 时,恒有
时,恒有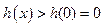
即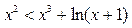 恒成立.取
恒成立.取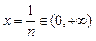 ,则有
,则有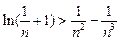 恒成立.
恒成立.
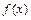 的定义域为
的定义域为 ,
,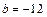 时,由
时,由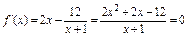 ,得
,得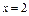 (
(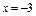 舍去),当x
舍去),当x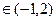 时,
时,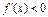 ,当
,当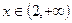 时,
时,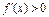 ,所以当
,所以当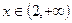 时,
时,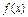 单调递增。
单调递增。(2)由题意
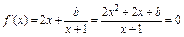 在
在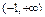 有两个不等实根,即
有两个不等实根,即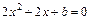 在
在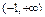 有两个不等实根,设
有两个不等实根,设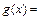
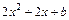 ,则
,则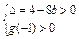 ,解之得
,解之得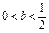
(3)对于函数
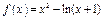 ,令函数
,令函数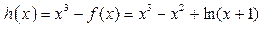
则
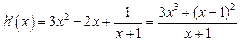 ,
,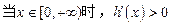 ,所以函数
,所以函数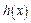 在
在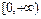 上单调递增,又
上单调递增,又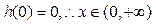 时,恒有
时,恒有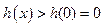
即
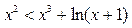 恒成立.取
恒成立.取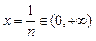 ,则有
,则有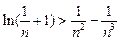 恒成立.
恒成立.
练习册系列答案
相关题目
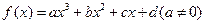 ,定义:设
,定义:设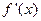 是函数
是函数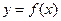 的导函数
的导函数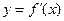 的导数,若
的导数,若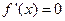 有实数解
有实数解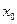 ,则称点
,则称点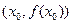 为函数
为函数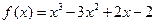 ,请解答下列问题:
,请解答下列问题: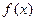 的“拐点”A的坐标;
的“拐点”A的坐标;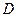 上的函数
上的函数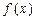 ,如果满
,如果满  ,
,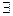 常数A,都有
常数A,都有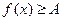 成立,则称函数
成立,则称函数 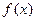 在区间
在区间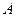 称为函数的下界. (提示:图(1)、(2)中的常数
称为函数的下界. (提示:图(1)、(2)中的常数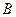 可以是正数,也可以是负数或零)
可以是正数,也可以是负数或零)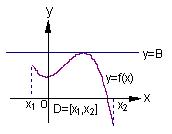 (Ⅰ)试判断函数
(Ⅰ)试判断函数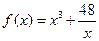 在
在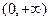 上是否有下界?并说明理由;
上是否有下界?并说明理由;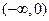 上是否
上是否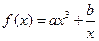 (
(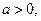
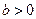
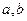 是常数)是否是
是常数)是否是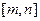 (
(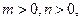
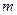 、
、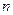 是常数)上的有界函数?
是常数)上的有界函数? (
(
 R).
R). 时,求函数
时,求函数 的极值;
的极值; 轴有且只有一个交点,求a的取值范围.
轴有且只有一个交点,求a的取值范围.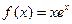 .
. (Ⅰ)求函数
(Ⅰ)求函数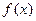 的单调区间;(Ⅱ)若常数
的单调区间;(Ⅱ)若常数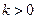 ,求不等式
,求不等式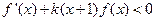 的解集.
的解集.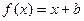 的图像与函数
的图像与函数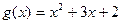 的图象相切,记
的图象相切,记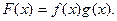
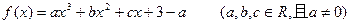 当
当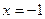 时,
时,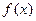 取得极大值2(1)用关于
取得极大值2(1)用关于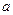 的代数式分别表示
的代数式分别表示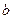 与
与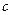 。(2)求
。(2)求 ,则
,则 = 。
= 。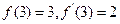 ,
,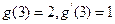 ,
,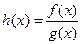 ,求
,求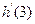 。
。