题目内容
(本小题满分16分)已知函数 是定义在
是定义在 上的奇函数,当
上的奇函数,当 时,
时,  (其中e是自然界对数的底,
(其中e是自然界对数的底, )(1)求
)(1)求 的解析式;(2)设
的解析式;(2)设 ,求证:当
,求证:当 时,
时, ;(3)是否存在实数a,使得当
;(3)是否存在实数a,使得当 时,
时, 的最小值是3 ?如果存在,求出实数a的值;如果不存在,请说明理由。
的最小值是3 ?如果存在,求出实数a的值;如果不存在,请说明理由。
 是定义在
是定义在 上的奇函数,当
上的奇函数,当 时,
时,  (其中e是自然界对数的底,
(其中e是自然界对数的底, )(1)求
)(1)求 的解析式;(2)设
的解析式;(2)设 ,求证:当
,求证:当 时,
时, ;(3)是否存在实数a,使得当
;(3)是否存在实数a,使得当 时,
时, 的最小值是3 ?如果存在,求出实数a的值;如果不存在,请说明理由。
的最小值是3 ?如果存在,求出实数a的值;如果不存在,请说明理由。(Ⅰ)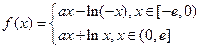 (Ⅲ)存在实数
(Ⅲ)存在实数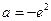 ,使得当
,使得当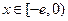 时,
时, 有最小值3
有最小值3
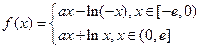 (Ⅲ)存在实数
(Ⅲ)存在实数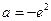 ,使得当
,使得当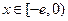 时,
时, 有最小值3
有最小值3(1)设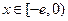 ,则
,则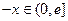 ,所以
,所以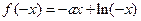
又因为 是定义在
是定义在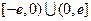 上的奇函数,所以
上的奇函数,所以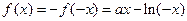
故函数 的解析式为
的解析式为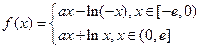 …4分
…4分
(2)证明:当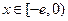 且
且 时,
时,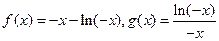 ,设
,设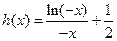
因为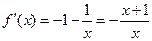 ,所以当
,所以当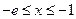 时,
时,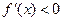 ,此时
,此时 单调递减;当
单调递减;当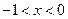 时,
时,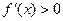 ,此时
,此时 单调递增,所以
单调递增,所以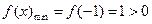
又因为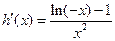 ,所以当
,所以当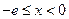 时,
时,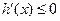 ,此时
,此时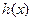 单调递减,所以
单调递减,所以
所以当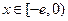 时,
时,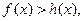 即
即 ……………………8分
……………………8分
(3)解:假设存在实数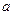 ,使得当
,使得当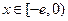 时,
时,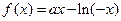 有最小值是3,则
有最小值是3,则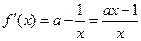
(ⅰ)当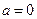 ,
,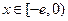 时,
时,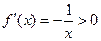 .
. 在区间
在区间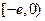 上单调递增,
上单调递增,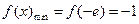 ,不满足最小值是3
,不满足最小值是3
(ⅱ)当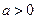 ,
,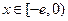 时,
时,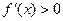 ,
, 在区间
在区间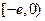 上单调递增,
上单调递增,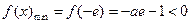 ,也不满足最小值是3
,也不满足最小值是3
(ⅲ)当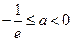 ,由于
,由于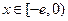 ,则
,则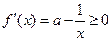 ,故函数
,故函数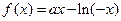 是
是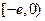 上的增函数.所以
上的增函数.所以 ,解得
,解得 (舍去)
(舍去)
(ⅳ)当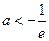 时,则当
时,则当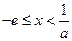 时,
时,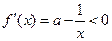 ,此时函数
,此时函数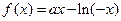 是减函数;
是减函数;
当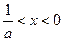 时,
时,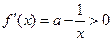 ,此时函数
,此时函数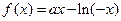 是增函数.
是增函数.
所以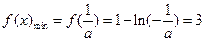 ,解得
,解得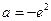
综上可知,存在实数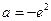 ,使得当
,使得当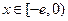 时,
时, 有最小值3 …………16分
有最小值3 …………16分
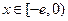 ,则
,则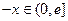 ,所以
,所以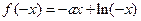
又因为
 是定义在
是定义在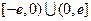 上的奇函数,所以
上的奇函数,所以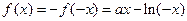
故函数
 的解析式为
的解析式为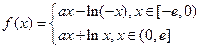 …4分
…4分(2)证明:当
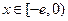 且
且 时,
时,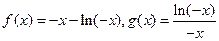 ,设
,设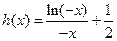
因为
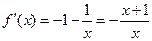 ,所以当
,所以当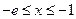 时,
时,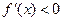 ,此时
,此时 单调递减;当
单调递减;当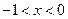 时,
时,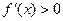 ,此时
,此时 单调递增,所以
单调递增,所以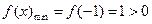
又因为
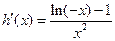 ,所以当
,所以当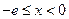 时,
时,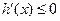 ,此时
,此时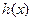 单调递减,所以
单调递减,所以
所以当
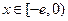 时,
时,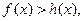 即
即 ……………………8分
……………………8分(3)解:假设存在实数
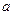 ,使得当
,使得当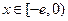 时,
时,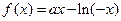 有最小值是3,则
有最小值是3,则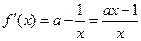
(ⅰ)当
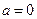 ,
,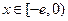 时,
时,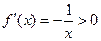 .
. 在区间
在区间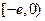 上单调递增,
上单调递增,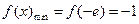 ,不满足最小值是3
,不满足最小值是3(ⅱ)当
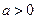 ,
,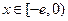 时,
时,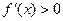 ,
, 在区间
在区间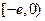 上单调递增,
上单调递增,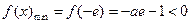 ,也不满足最小值是3
,也不满足最小值是3(ⅲ)当
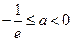 ,由于
,由于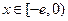 ,则
,则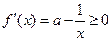 ,故函数
,故函数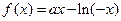 是
是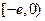 上的增函数.所以
上的增函数.所以 ,解得
,解得 (舍去)
(舍去)(ⅳ)当
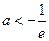 时,则当
时,则当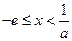 时,
时,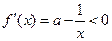 ,此时函数
,此时函数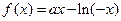 是减函数;
是减函数;当
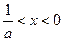 时,
时,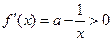 ,此时函数
,此时函数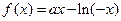 是增函数.
是增函数.所以
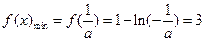 ,解得
,解得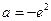
综上可知,存在实数
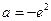 ,使得当
,使得当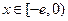 时,
时, 有最小值3 …………16分
有最小值3 …………16分
练习册系列答案
相关题目
 (
(
 R).
R). 时,求函数
时,求函数 的极值;
的极值; 轴有且只有一个交点,求a的取值范围.
轴有且只有一个交点,求a的取值范围.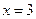 是函数
是函数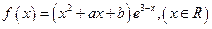 的一个极值点。
的一个极值点。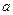 与
与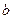 的关系式(用
的关系式(用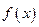 的单调区间;(2)设
的单调区间;(2)设 ,若存在
,若存在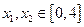 ,使得
,使得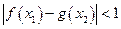 成立,求
成立,求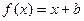 的图像与函数
的图像与函数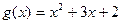 的图象相切,记
的图象相切,记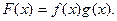
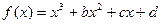 在(0,+
在(0,+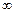 )上是增函数,在[–1,0]上是减函数,且方程
)上是增函数,在[–1,0]上是减函数,且方程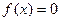 有三个根,它们分别为α,–1,β.
有三个根,它们分别为α,–1,β.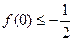 ;(3)求|α–β|的取值范围.
;(3)求|α–β|的取值范围.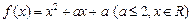 ,
,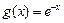 ,
,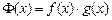 .
.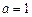 时,求
时,求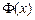 的单调区间;
的单调区间;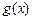 在点
在点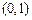 处的切线与直线
处的切线与直线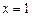 及曲线
及曲线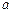 ,使
,使