题目内容
4.若函数f(x)=$\frac{ax+1}{x+2}$在(-2,2)内为增函数,则实数a的取值范围是( )| A. | ($\frac{1}{2}$,+∞) | B. | [$\frac{1}{2}$,+∞) | C. | (-∞,$\frac{1}{2}$) | D. | (-∞,$\frac{1}{2}$] |
分析 化简f(x)=$\frac{ax+1}{x+2}$=$\frac{a(x+2)+1-2a}{x+2}$=a+$\frac{1-2a}{x+2}$;从而由反比例函数可得1-2a<0;从而解得.
解答 解:f(x)=$\frac{ax+1}{x+2}$=$\frac{a(x+2)+1-2a}{x+2}$
=a+$\frac{1-2a}{x+2}$;
∵函数f(x)=$\frac{ax+1}{x+2}$在(-2,2)内为增函数,
∴1-2a<0;
解得,a>$\frac{1}{2}$;
故选:A.
点评 本题考查了函数的化简与反比例函数的应用,属于基础题.

练习册系列答案
相关题目
18.△ABC中,角A,B,C所对的边分别为a,b,c,若a=$\sqrt{7}$,b=3,c=2,则∠A=( )
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
19.已知随机变量ξ:B(10,0.04),随机变量ξ的数学期望E(ξ)=( )
| A. | 0.2 | B. | 0.4 | C. | 2 | D. | 4 |
12.设z1=-2i,z2=i-2,复数Z1和Z2在复平面内对应点分别为A、B,点O为原点,则△AOB的面积为( )
| A. | 1 | B. | 2 | C. | $\sqrt{2}$ | D. | 4 |
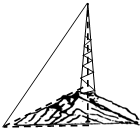 如图,某城市的电视发射塔CD建在市郊的小山上,小山的高BC为30米,在地面上
如图,某城市的电视发射塔CD建在市郊的小山上,小山的高BC为30米,在地面上