题目内容
13.f(x)=$\frac{{a•{4^x}-{a^{-2}}}}{{{4^x}+1}}$为定义在R上的奇函数(1)求a;
(2)设$h(x)={log_2}^{\frac{a+x}{a-x}},g(x)={log_{\sqrt{2}}}^{\frac{1+x}{k}}$,当$x∈[{\frac{1}{3}\;,\;\frac{2}{3}}]$时h(x)≤g(x)恒成立,求实数k的范围.
分析 (1)由奇函数的性质:f(0)=0,可得a=1,再由奇函数的定义,检验即可得到;
(2)运用对数函数的单调性,可得不等式即为$\frac{1+x}{1-x}$≤($\frac{1+x}{k}$)2,由题意可得k2≤1-x2在$x∈[{\frac{1}{3}\;,\;\frac{2}{3}}]$时恒成立.求得右边二次函数的最小值,即可得到k的范围.
解答 解:(1)f(x)=$\frac{{a•{4^x}-{a^{-2}}}}{{{4^x}+1}}$为定义在R上的奇函数,
即有f(0)=0,即a-a-2=0,
解得a=1,
则f(x)=$\frac{{4}^{x}-1}{{4}^{x}+1}$,f(-x)=$\frac{{4}^{-x}-1}{{4}^{-x}+1}$=$\frac{1-{4}^{x}}{1+{4}^{x}}$=-f(x),
f(x)为奇函数,
故a=1;
(2)h(x)=log2$\frac{1+x}{1-x}$,
h(x)≤g(x)恒成立,
即为log2$\frac{1+x}{1-x}$≤$lo{g}_{\sqrt{2}}\frac{1+x}{k}$=log2($\frac{1+x}{k}$)2,
即有$\frac{1+x}{1-x}$≤($\frac{1+x}{k}$)2,
由于$x∈[{\frac{1}{3}\;,\;\frac{2}{3}}]$,则k>0,
即有k2≤1-x2在$x∈[{\frac{1}{3}\;,\;\frac{2}{3}}]$时恒成立.
即有k2≤1-$\frac{4}{9}$=$\frac{5}{9}$,
解得0<k≤$\frac{\sqrt{5}}{3}$.
即有k的取值范围是(0,$\frac{\sqrt{5}}{3}$].
点评 本题考查函数的奇偶性的性质及运用,对数函数的单调性的运用,同时考查不等式恒成立问题注意转化为求函数的最值问题,考查运算能力,属于中档题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | ($\frac{1}{2}$,+∞) | B. | [$\frac{1}{2}$,+∞) | C. | (-∞,$\frac{1}{2}$) | D. | (-∞,$\frac{1}{2}$] |
| A. | 大前提 | B. | 小前提 | C. | 推理形式 | D. | 以上都是 |
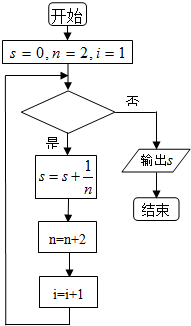
| A. | i≤11 | B. | i≤10 | C. | i≥10 | D. | i≥11 |
| A. | 既没有最大值也没有最小值 | B. | 有最大值5,没有最小值 | ||
| C. | 有最小值-1,没有最大值 | D. | 有最小值-5,也有最大值5 |
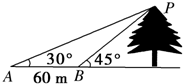 如图所示,为测一树的高度,在地面上选取A、B两点,从A、B两点分别测得树尖的仰角为30°,45°,且A、B两点之间的距离为60m,求树的高度.
如图所示,为测一树的高度,在地面上选取A、B两点,从A、B两点分别测得树尖的仰角为30°,45°,且A、B两点之间的距离为60m,求树的高度.