题目内容
9.已知向量$\overrightarrow a=({1,n}),\overrightarrow b=({-1,n})$,若$2\overrightarrow a-\overrightarrow b$与$\overrightarrow b$垂直,则$|{\overrightarrow a}|$=( )| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | 4 |
分析 运用坐标运算得出$2\overrightarrow a-\overrightarrow b$=(3,n),根据垂直得出($2\overrightarrow a-\overrightarrow b$)•$\overrightarrow b$=0,求解n2=3,就看得出模的值.
解答 解:∵向量$\overrightarrow a=({1,n}),\overrightarrow b=({-1,n})$,
∴$2\overrightarrow a-\overrightarrow b$=(3,n),
∵$2\overrightarrow a-\overrightarrow b$与$\overrightarrow b$垂直,
∴($2\overrightarrow a-\overrightarrow b$)•$\overrightarrow b$=0,
∴1×3+n2=0
即n2=3,
∴$|{\overrightarrow a}|$=$\sqrt{1+{n}^{2}}$=$\sqrt{4}$=2,
故选:C.
点评 本题考察了平面向量的坐标运算,考察了学生的计算能力,属于基础题.

练习册系列答案
相关题目
4.复数z=2-i(i是虚数单位)在复平面内对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
4.若函数f(x)=$\frac{ax+1}{x+2}$在(-2,2)内为增函数,则实数a的取值范围是( )
| A. | ($\frac{1}{2}$,+∞) | B. | [$\frac{1}{2}$,+∞) | C. | (-∞,$\frac{1}{2}$) | D. | (-∞,$\frac{1}{2}$] |
14.已知三角形△ABC中,角A,B,C的对边分别为a,b,c,若a=5,b=8,C=60°,则$\overrightarrow{BC}•\overrightarrow{AC}$=( )
| A. | $-20\sqrt{3}$ | B. | -20 | C. | 20 | D. | $20\sqrt{3}$ |
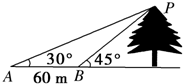 如图所示,为测一树的高度,在地面上选取A、B两点,从A、B两点分别测得树尖的仰角为30°,45°,且A、B两点之间的距离为60m,求树的高度.
如图所示,为测一树的高度,在地面上选取A、B两点,从A、B两点分别测得树尖的仰角为30°,45°,且A、B两点之间的距离为60m,求树的高度.