题目内容
【题目】某物流公司每天从甲地运货物到乙地,统计最近的200次可配送的货物量,可得可配送的货物量的频率分布直方图,所图所示,回答以下问题(直方图中每个小组取中间值作为该组数据的替代值).
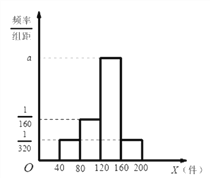
(1)求该物流公司每天从甲地到乙地平均可配送的货物量;
(2)该物流公司拟购置货车专门运营从甲地到乙地的货物,一辆货车每天只能运营一趟,每辆车每趟最多只能装载40件货物,满载发车,否则不发车.若发车,则每辆车每趟可获利1000元;若未发车,则每辆车每天平均亏损200元.为使该物流公司此项业务的营业利润最大,该物流公司应该购置几辆货车?
【答案】(1)125 (2) 3趟车
【解析】
试题分析:(1)由频率分布直方图的几何意义求出a的值,进而可得每组的频率,则可得![]() ;(2)由(1)可知从甲地到乙地的客流量在60,100,140,180的次数分别为25,50,100,25,依题意,讨论发发1趟车、2趟车、3趟车、4趟车,根据发车所获得的利润,求出每1种情况的平均利润即可.
;(2)由(1)可知从甲地到乙地的客流量在60,100,140,180的次数分别为25,50,100,25,依题意,讨论发发1趟车、2趟车、3趟车、4趟车,根据发车所获得的利润,求出每1种情况的平均利润即可.
试题解析:
(1)在区间![]() 的频率为
的频率为![]() ,
,
从甲地到乙地的客流量在![]() 的所占频率分别为
的所占频率分别为![]() .
.
从甲地到乙地的客流量在60,100,140,180的次数分别为25,50,100,25.
从甲地到乙地每天的平均客流量为:
![]() .
.
(2)由(1)可知从甲地到乙地的客流量在60,100,140,180的次数分别为25,50,100,25,依题意
(i)若发1趟车,则运输公司每天的营业利润值为1000;
(ii)若发2趟车,则每天的营业利润值的可能取值为2000,800,其次数分别为175,25
故平均利润值为![]() ;
;
(iii)若发3趟车,则每天的营业利润值的可能取值为3000,1800,600,其次数分别为125,50,25
故平均利润值为![]() ;
;
(iiii)若发4趟车,则每天的营业利润值的可能取值为4000,2800,1600,400其次数分别为25,100,50,25,
故平均利润值为![]() ;
;
因为2400>2350>1850>1000,
所以为使运输公司每天的营业利润最大,该公司每天应该发3趟车.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某种产品的质量按照其质量指标值M进行等级划分,具体如下表:
质量指标值M |
|
|
|
等级 | 三等品 | 二等品 | 一等品 |
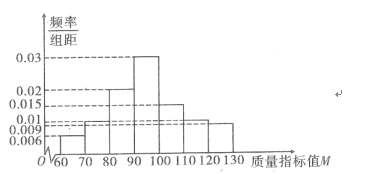
现从某企业生产的这种产品中随机抽取了100件作为样本,对其质量指标值M进行统计分析,得到如图所示的频率分布直方图.
(1)记A表示事件“一件这种产品为二等品或一等品”,试估计事件A的概率;
(2)已知该企业的这种产品每件一等品、二等品、三等品的利润分别为10元、6元、2元,试估计该企业销售10000件该产品的利润;
(3)根据该产品质量指标值M的频率分布直方图,求质量指标值M的中位数的估计值(精确到0.01)