题目内容
(本小题满分14分)已知数列{an}的前n项和为Sn,且an是Sn与2的等差中项,数列{bn}中,b1=1, 点P(bn,bn+1)在直线x-y+2=0上。
(1)求a1和a2的值; (2)求数列{an},{bn}的通项an和bn;
(1)求a1和a2的值; (2)求数列{an},{bn}的通项an和bn;
解:(1)∵an是Sn与2的等差中项 ∴Sn=2an-2 ∴a1=S1=2a1-2,解得a1=2
a1+a2=S2=2a2-2,解得a2="4"
(2)∵Sn=2an-2,Sn-1=2an-1-2,又Sn—Sn-1=an,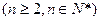 ∴an=2an-2an-1, ∵an≠0,
∴an=2an-2an-1, ∵an≠0,
∴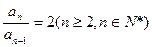 ,即数列{an}是等比数列 ∵a1=2,∴an=2n
,即数列{an}是等比数列 ∵a1=2,∴an=2n
∵点P(bn,bn+1)在直线x-y+2=0上,∴bn-bn+1+2=0,
∴bn+1-bn=2,即数列{bn}是等差数列,又b1=1,∴bn=2n-1
a1+a2=S2=2a2-2,解得a2="4"
(2)∵Sn=2an-2,Sn-1=2an-1-2,又Sn—Sn-1=an,
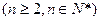 ∴an=2an-2an-1, ∵an≠0,
∴an=2an-2an-1, ∵an≠0,∴
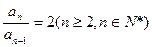 ,即数列{an}是等比数列 ∵a1=2,∴an=2n
,即数列{an}是等比数列 ∵a1=2,∴an=2n∵点P(bn,bn+1)在直线x-y+2=0上,∴bn-bn+1+2=0,
∴bn+1-bn=2,即数列{bn}是等差数列,又b1=1,∴bn=2n-1
略

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
 已知数列
已知数列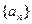 ,其前n项和
,其前n项和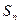 ,满足
,满足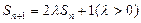 ,且
,且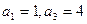
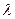 的值;
的值;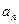 ;
;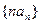 的前
的前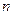 项和为
项和为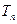 ,试比较
,试比较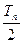 与
与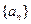 中
中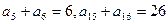 ,那么
,那么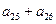 的值是_______________
的值是_______________ 是首项
是首项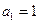 的等差数列,其前n项和为
的等差数列,其前n项和为 ,
,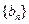 是首项
是首项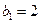 的等比数列,且
的等比数列,且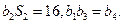
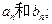
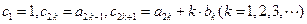 ,若数列
,若数列 的前n项和为
的前n项和为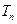 ,试比较
,试比较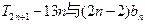 的大小。
的大小。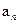 }从第一项开
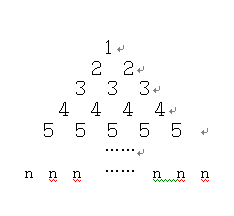
}从第一项开 始按照从上到下,从左到右的规律排列成如图所示的“三角阵”,即第一行是1个1,第二行是2个2,第三行是3个3,……,第n行是n个n(
始按照从上到下,从左到右的规律排列成如图所示的“三角阵”,即第一行是1个1,第二行是2个2,第三行是3个3,……,第n行是n个n( )
)
 1项
1项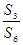 =
= ,则
,则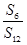 =( )
=( )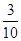
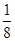
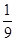
 列,而1,y1,y2,8依次成等比数列,则△OP1P2的面
列,而1,y1,y2,8依次成等比数列,则△OP1P2的面