题目内容

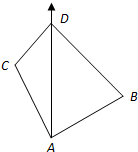
在△ABC中，已知角B=45°，D是BC边上一点，AD=5，AC=7，DC=3，求AB?
如题图，在△ACD中，由余弦定理可得cos∠ADC=
52+32-72
2×5×3
=-
1
2
．
∵0°＜∠ADC＜180°，∴∠ADC=120°，∴∠ADB=60°．
在△ABD中，由正弦定理可得
AB
sin60°
=
5
sin45°
，解得AB=
5
6
2
．
∴AB=
5
6
2
．
练习册系列答案
相关题目
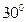如图，海平面上的甲船位于中心O的南偏西，与O相距10海里的C处，现甲船以30海里/小时的速度沿直线CB去营救位于中心O正东方向20海里的B处的乙船，甲船需要           小时到达B处.
如图，某货轮在A处看灯塔B在货轮的北偏东75°，距离18
6
海里，在A处看灯塔C在货轮的北偏西30°，距离为12
3
海里，货轮由A处向正北航行到D处时，再看灯塔B在北偏东120°，求：
（1）A处与D处的距离；
（2）灯塔C与D处的距离．
在△ABC中，已知a2+b2=c2+
2
ba，则∠C=（　　）
A．30°B．150°C．45°D．135°
已知函数f(x)=cos2x+2
3
sinxcosx-sin2x．
（Ⅰ）求f（x）的最小正周期和值域；
（Ⅱ）在△ABC中，角A，B，C所对的边分别是a，b，c，若f(
A
2
)=2且a2=bc，试判断△ABC的形状．
已知△ABC的内角A、B、C所对的边分别为a，b，c，且a=2．
（1）若b=2
3
，角A=30°，求角B的值；
（2）若△ABC的面积S△ABC=3，cosB=
4
5
，求b，c的值．
等腰三角形腰长是底边长的2倍，则顶角的余弦值是（　　）
A．
7
8
B．
2
2
3
C．
8
9
D．
7
9
在△ABC中，角A，B，C的对边分别为a，b，c，且a2+c2-b2=
2
3
3
acsinB．
（1）求角B的大小；
（2）若b=
3
，且A∈(
π
6
，
π
2
)，求a+c的取值范围．
设P是60°的二面角α-l-β内一点，PA⊥α，PB⊥β，A、B分别为垂足，PA=2，PB=4，则AB的长是 ______．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网