题目内容
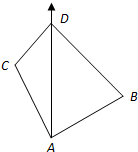
如图，某货轮在A处看灯塔B在货轮的北偏东75°，距离18
海里，在A处看灯塔C在货轮的北偏西30°，距离为12
海里，货轮由A处向正北航行到D处时，再看灯塔B在北偏东120°，求：
（1）A处与D处的距离；
（2）灯塔C与D处的距离．
| 6 |
| 3 |
（1）A处与D处的距离；
（2）灯塔C与D处的距离．
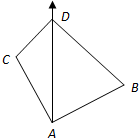
（1）设AD=x，由题意知∠DAB=75°，∠ADB=60°，∠ABD=45°，
由正弦定理得：
=
，
即
=
，
x=
=36
即x=36，
答：A、D两处相距36海里．
（2）设CD=y，由余弦定理可得：y2=362+(12
)2-2×36×12
cos30°=1296+432-1296=432，
∴y=12
答：灯塔C与D处的距离为12
海里．
由正弦定理得：
| x |
| sin45° |
18
| ||
| sin60° |
即
| x | ||||
|
18
| ||||
|
x=
| ||||||
|
即x=36，
答：A、D两处相距36海里．
（2）设CD=y，由余弦定理可得：y2=362+(12
| 3 |
| 3 |
∴y=12
| 3 |
答：灯塔C与D处的距离为12
| 3 |
练习册系列答案
相关题目
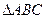中，已知
，则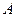
等于 （ ）
