题目内容
【题目】已知函数f（x）=x2e2x+m|x|ex+1（m∈R）有四个零点，则m的取值范围为（ ）
A.（﹣∞，﹣e﹣ 
）
B.（﹣∞，e+ ）
C.（﹣e﹣ ，﹣2）
D.（﹣∞，﹣ ）
【答案】A
【解析】解：令y=xex ， 则y'=（1+x）ex ， 由y'=0，得x=﹣1， 当x∈（﹣∞，﹣1）时，y'＜0，函数y单调递减，
当x∈（﹣1，+∞）时，y'＞0，函
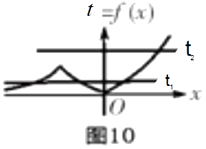
数y单调递增．作出y=xex图象，
利用图象变换得f（x）=|xex|图象（如图10），
令f（x）=t，则关于t方程h（t）=t2+mt+1=0两根分别在 
时（如图11），
满足g（x）=﹣1的x有4个，由 
，
解得m＜﹣e﹣ 
．
故选：A．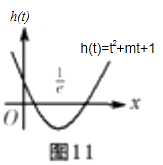
【考点精析】本题主要考查了利用导数研究函数的单调性的相关知识点，需要掌握一般的,函数的单调性与其导数的正负有如下关系： 在某个区间
内，(1)如果
，那么函数
在这个区间单调递增；(2)如果
，那么函数
在这个区间单调递减才能正确解答此题．
练习册系列答案
相关题目
【题目】某赛季甲、乙两名篮球运动员每场比赛得分的茎叶图如图所示，考虑以下结论：
甲 | 乙 | ||||||||
8 | 0 | ||||||||
4 3 3 | 6 6 8 | 3 8 9 1 | 1 2 3 4 5 | 2 5 1 4 0 | 5 4 6 9 | 1 | 6 | 7 | 9 |
①甲运动员得分的中位数大于乙运动员
得分的中位数；
②甲运动员得分的中位数小于乙运动员
得分的中位数；
③甲运动员得分的标准差大于乙运动员
得分的标准差；
④甲运动员得分的标准差小于乙运动员
得分的标准差；
其中根据茎叶图能得到的正确结论的编号为( )
A. ①③ B. ①④
C. ②③ D. ②④
