题目内容
【题目】已知函数
，若关于
的方程
有
个不同实数根，则n的值不可能为（ ）
A. 3 B. 4 C. 5 D. 6
【答案】A
【解析】
先将函数
写成分段函数的形式，并做出其图像，再由
得：
或
，所以方程的解的个数，即转化为函数
与
轴以及直线
交点个数的问题，由图像讨论
的范围，即可求出结果.
因为函数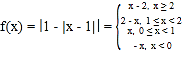
，
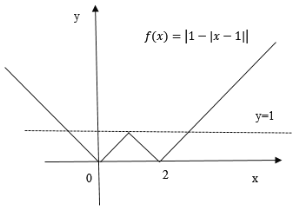
作出的图像如下：
由得：或，
所以方程的解的个数，即为函数与轴以及直线交点个数，
由图像可得：与轴有2个交点，
①当
,即
时，函数与直线无交点，故原方程共2个解；
②当
，即
时，原方程可化为，故原方程共2个解；
③当
，即
时，函数与直线有4个交点，故原方程共6个解；
④当
，即
时，函数与直线有3个交点，故原方程共5个解；
⑤当
，即
时，函数与直线有2个交点，故原方程共4个解；
综上，原方程解的个数可能为2,4,5,6.
故选A
练习册系列答案
名校课堂系列答案
相关题目
