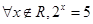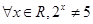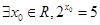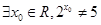题目内容
已知p:|1-
|≤2,q:[x-(1+m)]•[x-(1-m)]≤0(m>0),若p是q的充分而不必要条件,则实数m的取值范围是______.
| x-1 |
| 3 |
不等式|1-
|≤2可化为|x-4|<6,解得-2<x<10,
同理可解[x-(1+m)]•[x-(1-m)]≤0,得1-m<x<1+m,
要使p是q的充分而不必要条件,
需使{x|-2<x<10}是{x|1-m<x<1+m}的真子集,
故
,解不等式组可得m≥9,
经验证m=9满足题意,
故实数m的取值范围是:[9,+∞)
故答案为:[9,+∞)
| x-1 |
| 3 |
同理可解[x-(1+m)]•[x-(1-m)]≤0,得1-m<x<1+m,
要使p是q的充分而不必要条件,
需使{x|-2<x<10}是{x|1-m<x<1+m}的真子集,
故
|
经验证m=9满足题意,
故实数m的取值范围是:[9,+∞)
故答案为:[9,+∞)

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
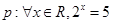 ,则
,则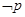 为( )
为( )