Question

12．如图，抛物线y=ax²+bx+3与x轴相交于点A（-1，0）、B（3，0），与y轴相交于点C，点P为线段OB上的动点（不与O、B重合），过点P垂直于x轴的直线与抛物线及线段BC分别交于点E、F，点D在y轴正半轴上，OD=2，连接DE、OF．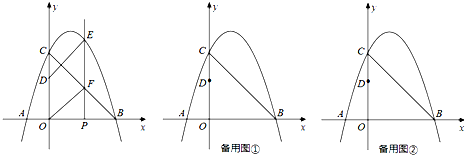

（1）求抛物线的解析式；
（2）当四边形ODEF是平行四边形时，求点P的坐标；
（3）过点A的直线将（2）中的平行四边形ODEF分成面积相等的两部分，求这条直线的解析式．（不必说明平分平行四边形面积的理由）

Answer 1

分析 （1）把点A、B的坐标代入抛物线方程，求出a、b的值即可；
（2）解法一，设出点P的坐标，利用抛物线与直线BC的解析式，以及平行四边形ODEF的关系，求出点P的坐标；
解法二，先求出点C的坐标与直线BC的解析式，利用平行四边形以及抛物线的性质，求出点P的坐标；
（3）结合图形，得出OP=2时，利用几何法求出平行四边形ODEF的中心，求出将平行四边形ODEF的面积等分的直线方程；
OP=1时，求出平行四边形ODEF的中心，求出将平行四边形ODEF的面积等分的直线方程．

解答 解：（1）∵抛物线y=ax²+bx+3与x轴相交于点A（-1，0）、B（3，0），
∴$\left\{\begin{array}{l}{a-b+3=0}\\{9a+3b+3=0}\end{array}\right.$，
解得a=-1，b=2，
∴抛物线方程为y=-x²+2x+3；
（2）解法一：设点P（m，0），∵点E在抛物线y=-x²+2x+3上，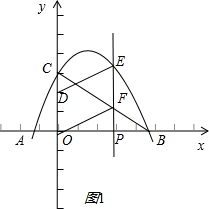

∴PE=-m²+2m+3，
把x=0代入y=-x²+2x+3，得y=3；
∴C（0，3）；
设直线BC的解析式为y=kx+b，则
$\left\{\begin{array}{l}{3k+b=0}\\{b=3}\end{array}\right.$，解得k=-1，b=3；
∴直线BC的解析式为y=-x+3，如图1；
∵点F在直线BC上，∴PF=-m+3；
∴EF=PE-PF=-m²+3m，
若四边形ODEF是平行四边形，则EF=OD=2；

∴-m²+3m=2，
解得m₁=1，m₂=2；
∴P（1，0）或 P（2，0）；
解法二：如图2，
把x=0代入y=-x²+2x+3，得y=3，
∴C（0，3）；
设直线BC的解析式为y=kx+b，
则$\left\{\begin{array}{l}{3k+b=0}\\{b=3}\end{array}\right.$，
解得k=-1，b=3，
∴直线BC的解析式为y=-x+3；
过点D作DG⊥EF于点G，则四边形ODGP是矩形，
∴DG=OP；
若四边形ODEF是平行四边形，∴DE∥OF，
∴∠DEF=∠OFP，
∵∠DGE=∠OPF=90°，
∴△DEG≌△OFP，
∴EG=FP；
设点P（m，0），∵点P在抛物线y=-x²+2x+3上，
∴PE=-m²+2m+3，
∵点F在直线BC上，∴PF=-m+3；
∵EG=-m²+2m+3-2=-m²+2m+1，
∴-m²+2m+1=-m+3，
∴-m²+3m-2=0，
解得m₁=1，m₂=2，
∴P（1，0）或 P（2，0）；

（3）当点P（2，0）时，即OP=2，如图3；
连接DF、OE相交于点G，取OP的中点H，连接GH，
∵四边形ODEF是平行四边形，
∴OG=GE，
∴GH是△OEP的中位线，
∴GH∥EP，GH=$\frac{1}{2}$PE，
把x=2代入y=-x²+2x+3，得y=3，即PE=3；
∴GH=$\frac{3}{2}$，
∵GH∥EP，
∴GH⊥OP，
∴G（1，$\frac{3}{2}$），
设直线AG的解析式为y=k₁x+b₁，则
$\left\{\begin{array}{l}{{k}_{1}{+b}_{1}=\frac{3}{2}}\\{{-k}_{1}{+b}_{1}=0}\end{array}\right.$，
解得k₁=b₁=$\frac{3}{4}$；
∴将平行四边形ODEF的面积等分的直线解析式为y=$\frac{3}{4}$x+$\frac{3}{4}$；
当点P（1，0）时，即OP=1，如图4；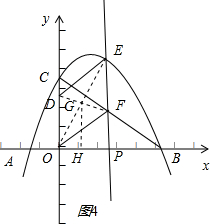
连接DF、OE相交于点G，取OP的中点H，连接GH；
∵四边形ODEF是平行四边形，
∴OG=GE，
∵OH=HP=$\frac{1}{2}$OP=$\frac{1}{2}$，
∴GH是△OEP的中位线，
∴GH∥EP，GH=$\frac{1}{2}$PE；
把x=1代入y=-x²+2x+3，得y=4，即PE=4；
∴GH=2，
∵GH∥EP，∴∠GHO=∠EPO=90°，
∴G（$\frac{1}{2}$，2）；
设直线AG的解析式为y=k₂x+b₂，则
$\left\{\begin{array}{l}{{\frac{1}{2}k}_{2}{+b}_{2}=2}\\{{-k}_{2}{+b}_{2}=0}\end{array}\right.$，
解得k₂=b₂=$\frac{4}{3}$，
∴将平行四边形ODEF的面积等分的直线解析式为y=$\frac{4}{3}$x+$\frac{4}{3}$；
综上所述，直线的解析式为y=$\frac{3}{4}$x+$\frac{3}{4}$或y=$\frac{4}{3}$x+$\frac{4}{3}$．

点评 本题考查了用待定系数法求函数的解析式的问题，也考查了直线与抛物线的综合应用问题，也考查了平行四边形的性质与应用问题，是综合性题目．