题目内容
【题目】四棱锥![]() 中,
中,![]() 平面
平面![]() ,底面四边形
,底面四边形![]() 为直角梯形,
为直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() .
.
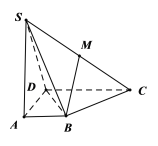
(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值;
的余弦值;
(Ⅲ)![]() 为
为![]() 中点,在四边形
中点,在四边形![]() 所在的平面内是否存在一点
所在的平面内是否存在一点![]() ,使得
,使得![]() 平面
平面![]() ,若存在,求三角形
,若存在,求三角形![]() 的面积;若不存在,请说明理由.
的面积;若不存在,请说明理由.
【答案】(I)详见解析;(II)![]() ;(III)存在,理由见解析,三角形
;(III)存在,理由见解析,三角形![]() 的面积为
的面积为![]() .
.
【解析】
(I)通过证明![]() ,证得
,证得![]() 平面
平面![]() ,由此证得平面
,由此证得平面![]() 平面
平面![]() .
.
(II)建立空间直角坐标系,利用平面![]() 和平面
和平面![]() 的法向量,求得二面角
的法向量,求得二面角![]() 的余弦值.
的余弦值.
(III)先假设存在符合题意的![]() ,然后利用向量的数量积运算,求得
,然后利用向量的数量积运算,求得![]() 点的坐标,由此证得
点的坐标,由此证得![]() 点存在,并求得三角形
点存在,并求得三角形![]() 的面积.
的面积.
(I)由于![]() 平面
平面![]() ,所以
,所以![]() ,由于
,由于![]() ,所以
,所以![]() 平面
平面![]() ,由于
,由于![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
(II)由已知条件可知![]() 两两垂直,以
两两垂直,以![]() 为原点建立空间直角坐标系,则
为原点建立空间直角坐标系,则
![]() ,
,![]() .依条件知
.依条件知![]() 是平面
是平面![]() 的一个法向量.设
的一个法向量.设![]() 是平面
是平面![]() 的法向量,
的法向量,![]() ,由
,由 ,令
,令![]() ,得
,得![]() .设二面角
.设二面角![]() 的平面角为
的平面角为![]() ,则
,则 .
.
(III)假设存在点![]() 满足条件,设
满足条件,设![]() ,则
,则![]() ,
,![]() ,所以
,所以 ,解得
,解得![]() ,所以存在
,所以存在![]() 满足条件,此时
满足条件,此时![]() .
.


【题目】小明家的晚报在下午![]() 任何一个时间随机地被送到,他们一家人在下午
任何一个时间随机地被送到,他们一家人在下午![]() 任何一个时间随机地开始晚餐.为了计算晚报在晚餐开始之前被送到的概率,某小组借助随机数表的模拟方法来计算概率,他们的具体做法是将每个1分钟的时间段看作个体进行编号,
任何一个时间随机地开始晚餐.为了计算晚报在晚餐开始之前被送到的概率,某小组借助随机数表的模拟方法来计算概率,他们的具体做法是将每个1分钟的时间段看作个体进行编号,![]() 编号为01,
编号为01,![]() 编号为02,依此类推,
编号为02,依此类推,![]() 编号为90.在随机数表中每次选取一个四位数,前两位表示晚报时间,后两位表示晚餐时间,如果读取的四位数表示的晚报晚餐时间有一个不符合实际意义,视为这次读取的无效数据(例如下表中的第一个四位数7840中的78不符合晚报时间).按照从左向右,读完第一行,再从左向右读第二行的顺序,读完下表,用频率估计晚报在晚餐开始之前被送到的概率为
编号为90.在随机数表中每次选取一个四位数,前两位表示晚报时间,后两位表示晚餐时间,如果读取的四位数表示的晚报晚餐时间有一个不符合实际意义,视为这次读取的无效数据(例如下表中的第一个四位数7840中的78不符合晚报时间).按照从左向右,读完第一行,再从左向右读第二行的顺序,读完下表,用频率估计晚报在晚餐开始之前被送到的概率为![]()
![]()
7840 1160 5054 3139 8082 7732 5034 3682 4829 4052 |
4201 6277 5678 5188 6854 0200 8650 7584 0136 7655 |
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()

