题目内容
已知函数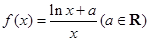 .
.
(1)求函数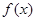 的单调区间和极值;
的单调区间和极值;
(2)当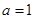 ,且
,且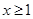 时,证明:
时,证明: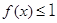 .
.
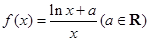 .
.(1)求函数
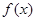 的单调区间和极值;
的单调区间和极值;(2)当
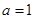 ,且
,且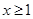 时,证明:
时,证明: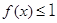 .
.(1)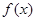 的单调递增区间是
的单调递增区间是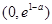 ,单调递减区间是
,单调递减区间是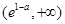 ,
, ;(2)证明见解析.
;(2)证明见解析.
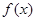 的单调递增区间是
的单调递增区间是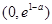 ,单调递减区间是
,单调递减区间是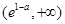 ,
, ;(2)证明见解析.
;(2)证明见解析.试题分析:(1)先求出
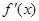 ,再根据
,再根据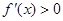 或
或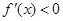 ,求得函数的单调区间和极值;(2)构造函数,利用最值即可证明不等式.
,求得函数的单调区间和极值;(2)构造函数,利用最值即可证明不等式.试题解析:(1)函数
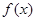 的定义域为
的定义域为 ,所以
,所以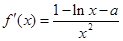 .
. 令
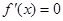 ,得
,得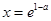 .
.当
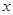 变化时,
变化时,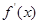 ,
,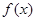 的变化情况如下表:
的变化情况如下表: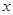 | 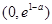 | 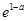 | 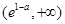 |
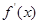 | 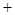 | 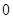 | 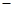 |
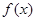 |  | 极大值 |  |
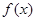 的单调递增区间是
的单调递增区间是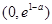 ,单调递减区间是
,单调递减区间是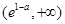 .
.所以
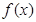 在
在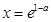 处取得极大值,
处取得极大值,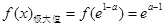 .
.(2)当
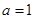 时,
时,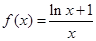 .
.令
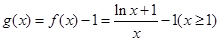 ,则
,则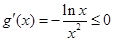 ,
,∴
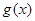 在
在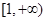 上单调递减,∴
上单调递减,∴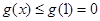 ,即
,即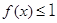 .
.
练习册系列答案
相关题目
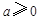 ,
,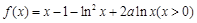 .
.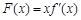 ,讨论
,讨论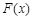 在
在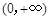 内的单调性并求极值;
内的单调性并求极值; 时,恒有
时,恒有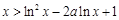 .
.
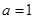 时,求
时,求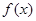 的极值;
的极值;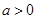 时,讨论
时,讨论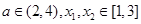 ,恒有
,恒有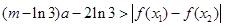 成立,求实数
成立,求实数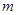 的取值范围.
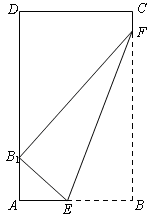
的取值范围.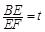 ,EF=l,l关于t的函数为
,EF=l,l关于t的函数为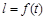 .
. 
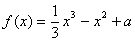 ,函数
,函数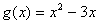 ,它们的定义域均为
,它们的定义域均为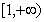 ,并且函数
,并且函数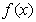 的图像始终在函数
的图像始终在函数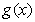 的上方,那么
的上方,那么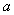 的取值范围是( )
的取值范围是( )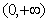
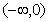
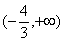
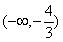
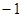 ,其中a≠0.若对一切x∈R,f(x)≥0恒成立,则a的取值集合 .
,其中a≠0.若对一切x∈R,f(x)≥0恒成立,则a的取值集合 .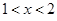 ,则
,则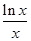 、
、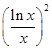 、
、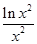 的大小关系是( )
的大小关系是( )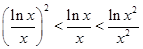
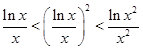
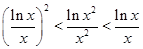
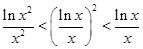
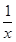 在
在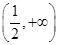 上是增函数,则a的取值范围是________.
上是增函数,则a的取值范围是________.