Question

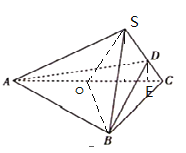
【题目】如图，在三棱锥中，，，，，.

（1）证明：平面平面；

（2）已知为棱上一点，若，求线段的长.

Answer 1

【答案】（1）见解析；（2）

【解析】

（1）取AC中点O，连结SO，BO，则SO＝BO＝1，且BO⊥AC，从而SO⊥BO，进而BO⊥平面SAC，由此能证明平面SAC⊥平面ABC；

（2）由D为棱SC上一点，四面体ABCD的体积为，过D作DE⊥AC，交AC于E，能求出点D到平面ABC的距离为DE，从而CE，进而AE＝2．由此能求出线段AD的长．

（1）在三棱锥S﹣ABC中，SA⊥SC，AB⊥BC，AB＝BC，SB＝，AC＝2，∠SAC＝30°．

取AC中点O，连结SO，BO，则SO＝BO＝1，且BO⊥AC，∴SO2+BO2＝SB2，∴SO⊥BO，

∵SO∩AC＝O，∴BO⊥平面SAC，∵BO平面ABC，∴平面SAC⊥平面ABC．

（2）D为棱SC上一点，四面体ABCD的体积为，

＝1，

过D作DE⊥AC，交AC于E，则点D到平面ABC的距离为DE＝h，

则VABCD＝＝＝，

解得DE＝h＝，∴CE＝＝，∴AE＝2﹣＝．

∴线段AD的长为：AD＝＝＝．