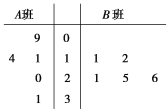
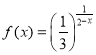题目内容
【题目】作出下列函数的大致图像,并写出函数的单调区间和值域:
(1)![]() ; (2)
; (2)![]() ;(3)
;(3)![]() ;
;
(4)![]() ;(5)
;(5)![]() ;(6)
;(6)![]() .
.
【答案】(1)减区间:![]() 和
和![]() ,值域:
,值域:![]() ;(2)减区间:
;(2)减区间:![]() 和
和![]() ,增区间:
,增区间:![]() 和
和![]() ,值域:
,值域:![]() ;(3)增区间:
;(3)增区间:![]() ,值域:R;(4)增区间:
,值域:R;(4)增区间:![]() 和
和![]() ,减区间:
,减区间:![]() ,值域:
,值域:![]() ;(5)减区间:
;(5)减区间:![]() 和
和![]() ,增区间:
,增区间:![]() 和
和![]() ,值域:
,值域:![]() ;(6)减区间:
;(6)减区间:![]() 和
和![]() ,增区间:
,增区间:![]() 和
和![]() ,值域:
,值域:![]() ,大致图像见解析
,大致图像见解析
【解析】
分别画出函数的图象,根据图象即可得到函数的单调区间和值域.
(1)![]() ,图象如图所示:
,图象如图所示:
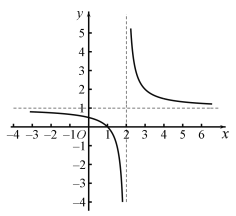
函数在![]() 和
和![]() 为减函数.
为减函数.
因为![]() ,所以
,所以![]() ,故值域为:
,故值域为:![]() ;
;
(2)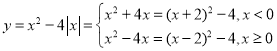 ,图象如图所示:
,图象如图所示:
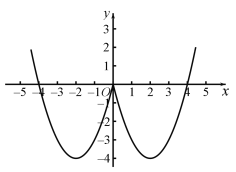
函数在![]() 和
和![]() 为减函数,在
为减函数,在![]() 和
和![]() 为增函数,
为增函数,
当![]() 时,
时,![]() 取得最小值
取得最小值![]() ,故值域:
,故值域:![]() ;
;
(3)函数![]() 的图象如图所示:
的图象如图所示:
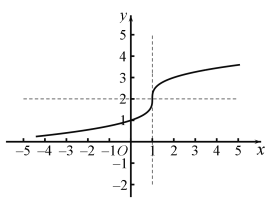
函数在![]() 上为增函数,值域:
上为增函数,值域:![]() .
.
(4)![]() ,图象如图所示:
,图象如图所示:
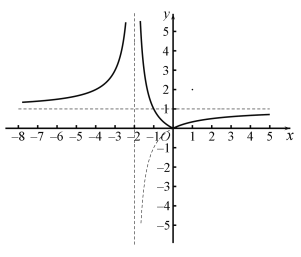
函数在![]() 和
和![]() 为增函数,在
为增函数,在![]() 为减函数,
为减函数,
值域为:![]() .
.
(5)![]() ,图象如图所示:
,图象如图所示:
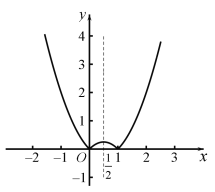
函数在![]() 和
和![]() 为减函数,在
为减函数,在![]() 和
和![]() 为增函数.
为增函数.
值域为:![]() ;
;
(6)![]()
,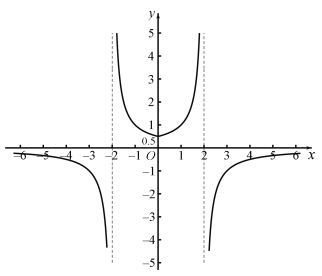
函数在![]() 和
和![]() 为减函数,在
为减函数,在![]() 和
和![]() 为增函数,
为增函数,
值域为:![]() .
.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
【题目】某商店为了解气温对某产品销售量的影响,随机记录了该商店![]() 月份中
月份中![]() 天的日销售量
天的日销售量![]() (单位:千克)与该地当日最低气温
(单位:千克)与该地当日最低气温![]() (单位:℃)的数据,如表所示:
(单位:℃)的数据,如表所示:
|
|
|
|
|
|
|
|
|
|
|
|
(1)求![]() 与
与![]() 的回归方程
的回归方程![]() :
:
(2)判断![]() 与
与![]() 之间是正相关还是负相关;若该地
之间是正相关还是负相关;若该地![]() 月份某天的最低气温为
月份某天的最低气温为![]() ,请用(1)中的回归方程预测该商店当日的销售量.
,请用(1)中的回归方程预测该商店当日的销售量.
参考公式: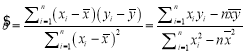 ,
,![]() .
.