题目内容
2.已知正方形ABCD的对角线交于点M,坐标原点不在正方形内部,且$\overrightarrow{OA}$=(0,3),$\overrightarrow{OD}$=(4,0),则向量$\overrightarrow{CM}$的坐标是($-\frac{7}{2},-\frac{1}{2}$).分析 设出C坐标,画出图形,利用向量与三角函数的关系,求出C的坐标,然后求解即可.
解答  解:设C(x,y),由题意可知:cos(β+$\frac{π}{2}$)=-|$\frac{OD}{AD}$|=$-\frac{4}{5}$,
解:设C(x,y),由题意可知:cos(β+$\frac{π}{2}$)=-|$\frac{OD}{AD}$|=$-\frac{4}{5}$,
sin(β+$\frac{π}{2}$)=$\left|\frac{OA}{AD}\right|$=$\frac{3}{5}$,
∴sinβ=$\frac{4}{5}$,cosβ=$\frac{3}{5}$
可得:x=4+5×cosβ=7,y=5sinβ=4,
C(7,4),
$\overrightarrow{CM}$=$\frac{1}{2}$$\overrightarrow{CA}$=$\frac{1}{2}$(-7,-1)=($-\frac{7}{2},-\frac{1}{2}$).
故答案为:($-\frac{7}{2},-\frac{1}{2}$).
点评 本题考查向量的综合应用,向量与三角函数的相结合,实际考查向量的旋转,考查分析问题解决问题的能力.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
12.已知不等式组$\left\{\begin{array}{l}{x+y≥4}\\{x-y≥-2}\\{x≤2}\end{array}\right.$,表示的平面区域为D,点O(0,0),A(1,0).若点M是D上的动点,则$\frac{\overrightarrow{OA}•\overrightarrow{OM}}{|\overrightarrow{OM|}}$的最小值是( )
| A. | $\frac{\sqrt{10}}{10}$ | B. | $\frac{\sqrt{5}}{5}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{3\sqrt{10}}{10}$ |
10.如图阴影部分的面积是( )
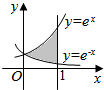

| A. | e+$\frac{1}{e}$ | B. | e+$\frac{1}{e}$-1 | C. | e+$\frac{1}{e}$-2 | D. | e-$\frac{1}{e}$ |
17.函数f(x)=x+2cosx在[0,π]上的极小值点为( )
| A. | 0 | B. | $\frac{π}{6}$ | C. | $\frac{5π}{6}$ | D. | π |
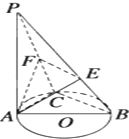 如图,PA⊥圆O所在的平面,AB是圆O的直径,C是圆O上的一点,E、F分别是点A在PB、PC上的射影,给出下列结论:
如图,PA⊥圆O所在的平面,AB是圆O的直径,C是圆O上的一点,E、F分别是点A在PB、PC上的射影,给出下列结论: